题目内容
【题目】在四面体ABCD中,二面角A﹣BC﹣D为60°,点P为直线BC上一动点,记直线PA与平面BCD所成的角为θ,则( ) 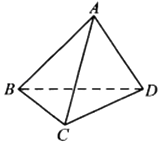
A.θ的最大值为60°
B.θ的最小值为60°
C.θ的最大值为30°
D.θ的最小值为30°
【答案】A
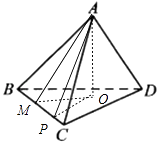
【解析】解:过A作AM⊥BC,AO⊥平面BCD,垂足为O,连结OM,
则∠AMO为二面角A﹣BC﹣D的平面角,∴∠AMO=60°,
在直线BC上任取一点P,连结OP,AP,
则∠APO为直线AP与平面BCD所成的角,即∠APO=θ,
∵AP≥AM,AMsin60°=AO,APsinθ=AO,
∴sinθ≤sin60°,即θ的最大值为60°.
故选A.
【考点精析】本题主要考查了空间角的异面直线所成的角的相关知识点,需要掌握已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则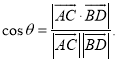 才能正确解答此题.
才能正确解答此题.

练习册系列答案
相关题目


