题目内容
13.下列4个命题,其中正确的命题序号为( )①|x+$\frac{1}{x}$|的最小值是2 ②$\frac{{x}^{2}+2}{\sqrt{{x}^{2}+1}}$的最小值是2 ③log2x+logx2的最小值是2 ④3x+3-x的最小值是2.
| A. | ①②③ | B. | ①②④ | C. | ②③④ | D. | ①③④ |
分析 根据基本不等式的性质分别对①②③④进行判断即可.
解答 解:①x>0时,|x+$\frac{1}{x}$|=x+$\frac{1}{x}$≥2$\sqrt{x•\frac{1}{x}}$=2,
当且仅当x=1时,“=”成立,
x<0时,|x+$\frac{1}{x}$|=-x-$\frac{1}{x}$≥2$\sqrt{(-x)•(-\frac{1}{x})}$,
当且仅当x=-1时,“=”成立,
故①正确;
②$\frac{{x}^{2}+2}{\sqrt{{x}^{2}+1}}$=$\frac{{x}^{2}+1+1}{\sqrt{{x}^{2}+1}}$=$\sqrt{{x}^{2}+1}$+$\frac{1}{\sqrt{{x}^{2}+1}}$≥2,
当且仅当x=0时,“=”成立,
故②正确;
③当0<x<1时,log2x+logx2的和是负数,
故③错误;
④3x+3-x=3x+$\frac{1}{{3}^{x}}$≥2$\sqrt{{3}^{x}•\frac{1}{{3}^{x}}}$=2,
当且仅当x=0时,“=”成立,
故选:B.
点评 本题考查了基本不等式的性质的应用,熟练掌握满足基本不等式的条件是解答本题的关键,本题是一道基础题.

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案
相关题目
8.若(2+x)7=a0+a1(x+1)+a2(x+1)2+…+a7(x+1)7,则a1+a3+a5+a7等于( )
| A. | $\frac{127}{2}$ | B. | $\frac{255}{2}$ | C. | 64 | D. | 128 |
18.执行如图所示的程序框图,如果输入的N=5,那么输出的S等于( )
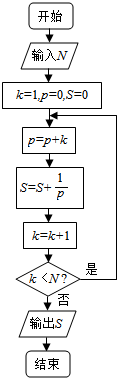

| A. | $\frac{7}{4}$ | B. | $\frac{8}{5}$ | C. | $\frac{16}{9}$ | D. | $\frac{20}{11}$ |
5.在△ABC中,若sin(A-B)=1+2cos(B+C)sin(A+C),则△ABC的形状一定是( )
| A. | 等边三角形 | B. | 不含60°的等腰三角形 | ||
| C. | 钝角三角形 | D. | 直角三角形 |
2.化简(x+1)4-4(x+1)3+6(x+1)2-4(x+1)+1的结果为( )
| A. | x4 | B. | (x-1)4 | C. | (x+1)4 | D. | x4-1 |
3.设a=0.82.1,b=21.1,c=log23,则( )
| A. | b<c<a | B. | c<a<b | C. | a<b<c | D. | a<c<b |