题目内容
【题目】已知抛物线y2=4 ![]() x的交点为椭圆
x的交点为椭圆 ![]() (a>b>0)的右焦点,且椭圆的长轴长为4,左右顶点分别为A,B,经过椭圆左焦点的直线l与椭圆交于C,D(异于A,B)两点.
(a>b>0)的右焦点,且椭圆的长轴长为4,左右顶点分别为A,B,经过椭圆左焦点的直线l与椭圆交于C,D(异于A,B)两点. 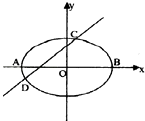
(1)求椭圆标准方程;
(2)求四边形ADBC的面积的最大值;
(3)若M(x1 , y1)N(x2 , y2)是椭圆上的两动点,且满x1x2+2y1y2=0,动点P满足 ![]() (其中O为坐标原点),是否存在两定点F1 , F2使得|PF1|+|PF2|为定值,若存在求出该定值,若不存在说明理由.
(其中O为坐标原点),是否存在两定点F1 , F2使得|PF1|+|PF2|为定值,若存在求出该定值,若不存在说明理由.
【答案】
(1)解:由题设知:抛物线y2=4 ![]() x的焦点为(
x的焦点为( ![]() ,0),
,0),
∴椭圆中的c= ![]() ,又由椭圆的长轴为4,得a=2,
,又由椭圆的长轴为4,得a=2,
∴b2=a2﹣c2=2,
∴椭圆方程为 ![]()
(2)解:设直线l:x=my﹣ ![]() ,代入椭圆方程,得:(m2+2)y2﹣2
,代入椭圆方程,得:(m2+2)y2﹣2 ![]() my﹣2=0,
my﹣2=0,
设C(x1,y1),D(x2,y2),A(﹣2,0),B(2,0),
y1+y2= ![]() ,y1y2=
,y1y2= ![]() ,判别式为(2
,判别式为(2 ![]() m)2+8(m2+2)>0,
m)2+8(m2+2)>0,
则四边形ADBC的面积S=S△ABC+S△ABD= ![]() |AB||y1﹣y2|=2
|AB||y1﹣y2|=2 ![]()
=2 ![]() =
= ![]() =
= ![]() ≤
≤ ![]() =4,
=4,
当且仅当 ![]() =
= ![]() 即m=0时,等号成立.
即m=0时,等号成立.
则四边形ADBC的面积的最大值为4
(3)解:存在两定点F1,F2使得|PF1|+|PF2|为定值.
设P(xP,yP),M(x1,y1),N(x2,y2).
由 ![]() ,得:
,得: ![]() ,①
,①
x1x2+2y1y2=0,②
M,N是椭圆上的点,
∴x12+2y12=4,x22+2y22=4,
由①②,得xp2+2yP2=(x1+2x1)2+2(y1+2y2)2
=(x12+2y12)+4(x22+2y22),
∴xP2+2yP2=20,即 ![]() ,
,
由椭圆定义知|PF1|+|PF2|为定值4 ![]()
【解析】(1)由已知条件得椭圆中的c= ![]() ,又由椭圆的长轴为4,由此能求出椭圆方程;(2)设直线l:x=my﹣
,又由椭圆的长轴为4,由此能求出椭圆方程;(2)设直线l:x=my﹣ ![]() ,代入椭圆方程,得(m2+2)y2﹣2
,代入椭圆方程,得(m2+2)y2﹣2 ![]() my﹣2=0,运用韦达定理和四边形ADBC的面积S=S△ABC+S△ABD=
my﹣2=0,运用韦达定理和四边形ADBC的面积S=S△ABC+S△ABD= ![]() |AB||y1﹣y2|,化简整理,运用基本不等式即可求得m=0时,取得最大值4;(3)设P(xP , yP),M(x1 , y1),N(x2 , y2).由
|AB||y1﹣y2|,化简整理,运用基本不等式即可求得m=0时,取得最大值4;(3)设P(xP , yP),M(x1 , y1),N(x2 , y2).由 ![]() ,运用向量的坐标运算,得
,运用向量的坐标运算,得 ![]() ,由椭圆定义知|PF1|+|PF2|为定值4
,由椭圆定义知|PF1|+|PF2|为定值4 ![]() .
.