题目内容
对于任意实数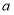 、
、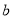 、
、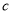 、
、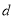 ,下列命题中,①若
,下列命题中,①若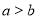 ,
,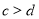 ,则
,则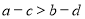 ;②若
;②若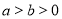 ,
,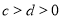 ,则
,则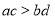 ;③若
;③若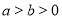 ,则
,则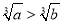 ④若
④若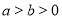 ,则
,则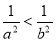
真命题的个数为 ( )
A.1 B.2 C.3 D.4
练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案
相关题目
题目内容
对于任意实数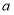 、
、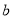 、
、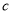 、
、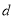 ,下列命题中,①若
,下列命题中,①若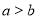 ,
,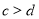 ,则
,则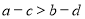 ;②若
;②若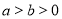 ,
,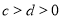 ,则
,则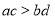 ;③若
;③若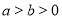 ,则
,则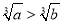 ④若
④若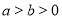 ,则
,则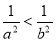
真命题的个数为 ( )
A.1 B.2 C.3 D.4
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案