题目内容
(本小题满分12分)
如图,正方形ABCD所在平面与平面四边形ABEF所在平面互相垂直,⊿ABE是等腰直角三角形,AB=AE,FA=FE,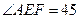 °
°

(1)求证:EF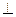 平面BCE;
平面BCE;
(2)求二面角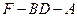 的大小。
的大小。
如图,正方形ABCD所在平面与平面四边形ABEF所在平面互相垂直,⊿ABE是等腰直角三角形,AB=AE,FA=FE,
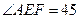 °
°
(1)求证:EF
 平面BCE;
平面BCE; (2)求二面角
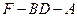 的大小。
的大小。(1)提示:因 为
为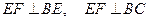 ,所以
,所以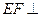 平面BCE
平面BCE
(2)解:建立如图所示的坐标系,设AB=AE=AD=1,
则B(0,1,0)、C(1,1,0)、D(1,0,0)、E(0,0,1)、F(0,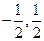 )
)
显然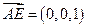 是平面ABD的一个法向量;
是平面ABD的一个法向量;
设平面BDF的一个法向量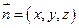
则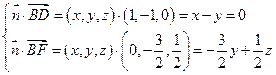 令
令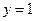 ,则
,则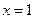 ,
,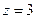 ,故
,故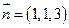
所以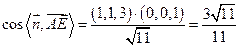
所以,二面角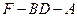 的大小为
的大小为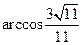
 为
为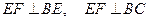 ,所以
,所以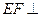 平面BCE
平面BCE(2)解:建立如图所示的坐标系,设AB=AE=AD=1,
则B(0,1,0)、C(1,1,0)、D(1,0,0)、E(0,0,1)、F(0,
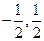 )
)显然
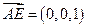 是平面ABD的一个法向量;
是平面ABD的一个法向量;设平面BDF的一个法向量
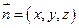
则
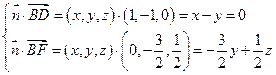 令
令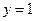 ,则
,则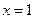 ,
,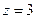 ,故
,故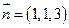
所以
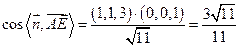
所以,二面角
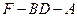 的大小为
的大小为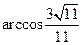
略

练习册系列答案
相关题目
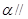 平面
平面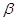 ,直线
,直线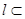 平面
平面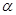 ,点
,点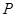
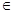 直线
直线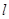 ,平面
,平面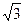 .
.
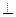 底面ABCD,PD=DC,
底面ABCD,PD=DC, 

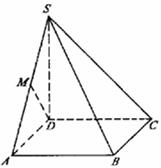
 的底面是正方形,且
的底面是正方形,且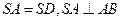 ,
,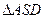 的面积为
的面积为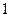 ,则能够放入这个棱锥的最大球的半径为
,则能够放入这个棱锥的最大球的半径为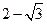
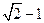

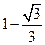
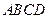 中,
中,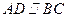 ,
,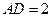 ,
,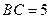 ,点
,点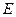 、
、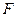 分别在
分别在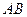 、
、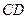 上,且
上,且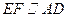 ,若
,若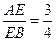 ,则
,则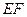 的长为 .
的长为 .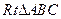 中
中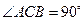 ,
,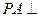 平面
平面 ,此图形中有 个直角三角形.
,此图形中有 个直角三角形.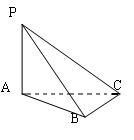
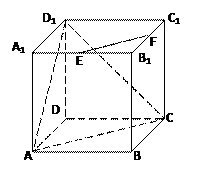
 平面
平面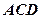 ,
,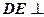 平面
平面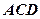 ,
,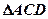 为
为 等边三角形,
等边三角形,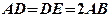 ,
,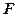 为
为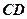 中点.
中点.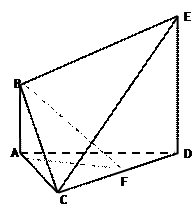
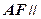 平面
平面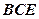 ;
;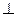 平面
平面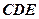 ;
;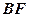 与平面
与平面
 的正弦值.
的正弦值.