Question

【题目】已知椭圆C：的左右焦点分别为F1，F2，点在椭圆C上，满足.

（1）求椭圆C的标准方程；

（2）直线l1过点P，且与椭圆只有一个公共点，直线l2与l1的倾斜角互补，且与椭圆交于异于点P的两点M，N，与直线x=1交于点K(K介于M，N两点之间).

①问：直线PM与PN的斜率之和能否为定值，若能，求出定值并写出详细计算过程；若不能，请说明理由；

②求证：.

Answer 1

【答案】（1）.（2）①定值为；②证明见解析

【解析】

（1）设F1 (﹣c,0),F2(c,0),由可求c=1,再把点P的坐标代入椭圆方程结合a2=b2+c2,即可求出a,b,c的值,从而得到椭圆C的标准方程；

（2）①显然直线l1的斜率存在,设直线l1的方程为：yk(x﹣1),与椭圆方程联立,利用△=0解出k的值,进而求出直线l2的斜率,设直线l2方程为：y,M(x1,y1),N(x2,y2),与椭圆方程联立,利用韦达定理代入kPM+kPN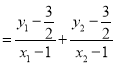,化简可得kPM+kPN=0为定值；②由①知∠MPK=∠NPK,

在△PMK和△PNK中,由正弦定理得,所以,即|PM||KN|=|PN||KM|成立.

（1）设F1 (﹣c,0),F2(c,0),c>0,则(﹣c﹣1,)(c﹣1,)=1﹣c2,

∴c=1,

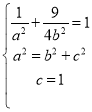∴,解得,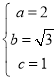

∴椭圆C的标准方程为：；

（2）①显然直线l1的斜率存在,设直线l1的方程为：yk(x﹣1),即y=k(x﹣1)

联立方程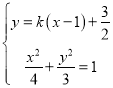,消去y得：(4k2+3)x2+(12k﹣8k2)x+(3﹣2k)2﹣12=0,

由题意可知△=(12k﹣8k2)2﹣4×(4k2+3)[(3﹣2k)2﹣12]=0,解得k,

∵直线l2与l1的倾斜角互补,∴直线l2的斜率为,

设直线l2方程为：y,M(x1,y1),N(x2,y2),

联立方程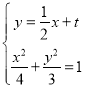,整理得x2+tx+t2﹣3=0,

由△=t2﹣4(t2﹣3)>0,得t2<4,

且x1+x2=﹣t,,

∴直线PM与PN的斜率之和kPM+kPN0；

②由①知PMPN关于直线x=1对称,即∠MPK=∠NPK,

在△PMK和△PNK中,由正弦定理得,

又因为∠MPK=∠NPK,∠PKM+∠PKN=180°,

∴,

∴|PM||KN|=|PN||KM|成立.