题目内容
6.设$\overrightarrow{a}$、$\overrightarrow{b}$、$\overrightarrow{c}$是非零向量,下列命题正确的是( )| A. | ($\overrightarrow{a}$•$\overrightarrow{b}$)•$\overrightarrow{c}$=$\overrightarrow{a}$•($\overrightarrow{b}$•$\overrightarrow{c}$) | B. | |$\overrightarrow{a}$-$\overrightarrow{b}$|2=|$\overrightarrow{a}$|2-2|$\overrightarrow{a}$||$\overrightarrow{b}$|+|$\overrightarrow{b}$|2 | ||
| C. | 若|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=|$\overrightarrow{a}$+$\overrightarrow{b}$|,则$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为60° | D. | 若|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=|$\overrightarrow{a}$-$\overrightarrow{b}$|,则$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为60° |
分析 运用向量的数量积的性质:向量的平方即为模的平方,以及向量的夹角的求法,即可判断A,B,C不正确,D正确.
解答 解:对于A,($\overrightarrow{a}$•$\overrightarrow{b}$)•$\overrightarrow{c}$为与$\overrightarrow{c}$共线的向量,$\overrightarrow{a}$•($\overrightarrow{b}$•$\overrightarrow{c}$)为与$\overrightarrow{a}$共线的向量,故A不正确;
对于B,|$\overrightarrow{a}$-$\overrightarrow{b}$|2=($\overrightarrow{a}$-$\overrightarrow{b}$)2=$\overrightarrow{a}$2-2$\overrightarrow{a}$•$\overrightarrow{b}$+$\overrightarrow{b}$2=|$\overrightarrow{a}$|2-2|$\overrightarrow{a}$|•|$\overrightarrow{b}$|cos<$\overrightarrow{a}$,$\overrightarrow{b}$>+|$\overrightarrow{b}$|2,故B不正确;
对于C,若|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=|$\overrightarrow{a}$+$\overrightarrow{b}$|,即有|$\overrightarrow{a}$|2=|$\overrightarrow{b}$|2=|$\overrightarrow{a}$+$\overrightarrow{b}$|2=$\overrightarrow{a}$2+2$\overrightarrow{a}$•$\overrightarrow{b}$+$\overrightarrow{b}$2,$\overrightarrow{a}$•$\overrightarrow{b}$=-$\frac{1}{2}$$\overrightarrow{a}$2,cos<$\overrightarrow{a}$,$\overrightarrow{b}$>=-$\frac{1}{2}$,
则$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为120°,故C不正确;
对于D,若|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=|$\overrightarrow{a}$-$\overrightarrow{b}$|,即有|$\overrightarrow{a}$|2=|$\overrightarrow{b}$|2=|$\overrightarrow{a}$-$\overrightarrow{b}$|2=$\overrightarrow{a}$2-2$\overrightarrow{a}$•$\overrightarrow{b}$+$\overrightarrow{b}$2,$\overrightarrow{a}$•$\overrightarrow{b}$=$\frac{1}{2}$$\overrightarrow{a}$2,cos<$\overrightarrow{a}$,$\overrightarrow{b}$>=$\frac{1}{2}$,
则$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为60°,故D正确.
故选D.
点评 本题考查向量的数量积的性质和夹角求法,属于中档题和易错题.

| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件 |
| A. | $\frac{3\sqrt{17}}{2}$ | B. | 2$\sqrt{10}$ | C. | $\frac{13}{2}$ | D. | 3$\sqrt{10}$ |
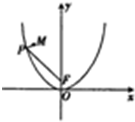 已知抛物线C:x2=2y的焦点为F,P为抛物线C上的任意一点,点M(-2,3),则|MP|+|PF|的最小值为$\frac{7}{2}$.
已知抛物线C:x2=2y的焦点为F,P为抛物线C上的任意一点,点M(-2,3),则|MP|+|PF|的最小值为$\frac{7}{2}$.