题目内容
某中学举行了一次“环保知识竞赛”活动.为了了解本次竞赛学生成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为100分)作为样本(样本容量为n)进行统计.按照 ,
, ,
, ,
, ,
, 的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在
的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在 ,
, 的数据).
的数据).
频率分布直方图 茎叶图
(Ⅰ)求样本容量n和频率分布直方图中x、y的值;
(Ⅱ)在选取的样本中,从竞赛成绩是80分以上(含80分)的同学中随机抽取2名同学到市政广场参加环保知识宣传的志愿者活动,求所抽取的2名同学来自不同组的概率.
(Ⅰ) ;(Ⅱ)
;(Ⅱ) .
.
解析试题分析:(Ⅰ)由频率分布直方图可求出分数在50到60的频率,由茎叶图可得出分数在50到60的人数,
由此可得样本容量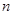 .又由茎叶图可得分数在90到100的人数,从而求得
.又由茎叶图可得分数在90到100的人数,从而求得 .这样除了60到70分这一组之外,其余各组的频率都知道了,也就可以求出
.这样除了60到70分这一组之外,其余各组的频率都知道了,也就可以求出 的值了.(Ⅱ)由(Ⅰ)可知,分数在[80,90)有5人,分数在[90,100)有2人,共7人.将这7人用不同字母表示出来,然后将取出2人所有基本事件(即可能出现的结果)一一列出,数出来自不同组的基本事件事件的个数,由古典概型的概率公式即得所求概率.
的值了.(Ⅱ)由(Ⅰ)可知,分数在[80,90)有5人,分数在[90,100)有2人,共7人.将这7人用不同字母表示出来,然后将取出2人所有基本事件(即可能出现的结果)一一列出,数出来自不同组的基本事件事件的个数,由古典概型的概率公式即得所求概率.
试题解析:(Ⅰ)由题意可知,样本容量 ,
, ,
, . 6分
. 6分
(Ⅱ)由题意可知,分数在[80,90)有5人,分别记为a,b,c,d,e,分数在[90,100)有2人,分别记为F,G.从竞赛成绩是80分以上(含80分)的同学中随机抽取2名同学有如下种情形:(a,b),(a,c),(a,d),(a,e),(a,F),(a,G),(b,c),(b,d),(b,e),(b,F),(b,G),(c,d),(c,e),(c,F),(c,G),(d,e),(d,F),(d,G),(e,F),(e,G),(F,G),共有21个基本事件;其中符合“抽取的2名同学来自不同组”的基本事件有(a,F),(a,G),(b,F),(b,G),(c,F),(c,G),(d,F),(d,G),(e,F),(e,G),共10个,
所以抽取的2名同学来自不同组的概率 . .12分
. .12分
考点:1、频率分布直方图与茎叶图;2、古典概型.

根据空气质量指数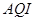 (为整数)的不同,可将空气质量分级如下表:
(为整数)的不同,可将空气质量分级如下表:
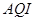 (数值) (数值) | 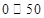 |  |  |  |  |  |
| 空气质量级别 | 一级 | 二级 | 三级 | 四级 | 五级 | 六级 |
| 空气质量类别 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
| 空气质量类别颜色 | 绿色 | 黄色 | 橙色 | 红色 | 紫色 | 褐红色 |
 年
年 月
月 日—
日— 月
月 日,对空气质量指数
日,对空气质量指数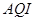 进行监测,获得数据后得到如图的条形图
进行监测,获得数据后得到如图的条形图
(1)估计该城市本月(按
 天计)空气质量类别为中度污染的概率;
天计)空气质量类别为中度污染的概率;(2)在空气质量类别颜色为紫色和褐红色的数据中任取
 个,求至少有一个数据反映的空气质量类别颜色为褐红色的概率.
个,求至少有一个数据反映的空气质量类别颜色为褐红色的概率. 电视传媒公司为了了解某地区电视观众对某类体育节目的收视情况,随机抽取了100名观众进行调查,其中女性有55名。右图是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图。将日均收看该体育节目时间不低于40分钟的观众称为“体育迷”,已知“体育迷”中有10名女性。
(Ⅰ)根据已知条件完成下面的2×2列联表,并据此资料判断你是否有95%以上的把握认为“体育迷”与性别有关?
| | 非体育迷 | 体育迷 | 合计 |
| 男 | | | |
| 女 | | | |
| 合计 | | | |



 的人群随机抽取
的人群随机抽取 人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图:
人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图:

 的值;
的值; 的“低碳族”中采用分层抽样法抽取6人参加户外低碳体验活动,其中选取2人作为领队,求选取的2名领队中恰有1人年龄在
的“低碳族”中采用分层抽样法抽取6人参加户外低碳体验活动,其中选取2人作为领队,求选取的2名领队中恰有1人年龄在 的概率.
的概率.
 ,求
,求 .
. 
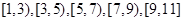 五组,画出的频率分布直方图如图所示.已知有4名学生的成绩在9米到11米之间.
五组,画出的频率分布直方图如图所示.已知有4名学生的成绩在9米到11米之间.
 的值及参加“掷铅球”项目测试的人数;
的值及参加“掷铅球”项目测试的人数;
 表示两人中成绩不合格的人数,求
表示两人中成绩不合格的人数,求