题目内容
已知函数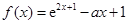 ,
,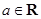 .
.
(Ⅰ)若曲线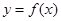 在点
在点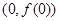 处的切线与直线
处的切线与直线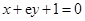 垂直,求
垂直,求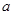 的值;
的值;
(Ⅱ)求函数 的单调区间;
的单调区间;
(Ⅲ)设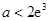 ,当
,当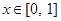 时,都有
时,都有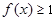 成立,求实数
成立,求实数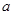 的取值范围.
的取值范围.
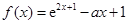 ,
,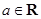 .
.(Ⅰ)若曲线
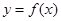 在点
在点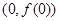 处的切线与直线
处的切线与直线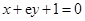 垂直,求
垂直,求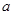 的值;
的值;(Ⅱ)求函数
 的单调区间;
的单调区间;(Ⅲ)设
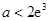 ,当
,当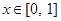 时,都有
时,都有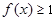 成立,求实数
成立,求实数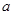 的取值范围.
的取值范围.(Ⅰ)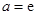 ,(Ⅱ)当
,(Ⅱ)当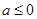 时,
时, 的单调增区间为
的单调增区间为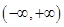 ;当
;当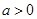 时,
时, 的单调增区间是
的单调增区间是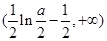 ,
, 的单调减区间是
的单调减区间是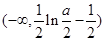 . (Ⅲ)
. (Ⅲ)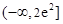 .
.
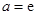 ,(Ⅱ)当
,(Ⅱ)当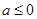 时,
时, 的单调增区间为
的单调增区间为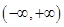 ;当
;当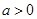 时,
时, 的单调增区间是
的单调增区间是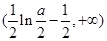 ,
, 的单调减区间是
的单调减区间是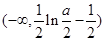 . (Ⅲ)
. (Ⅲ)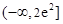 .
.试题分析:(Ⅰ)利用导数的几何意义,曲线
 在点
在点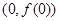 处的切线斜率为在点
处的切线斜率为在点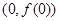 处的导数值. 由已知得
处的导数值. 由已知得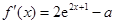 .所以
.所以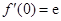 .
.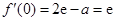 ,
,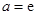 (Ⅱ)利用导数求函数单调区间,需明确定义域
(Ⅱ)利用导数求函数单调区间,需明确定义域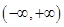 ,再导数值的符号确定单调区间. 当
,再导数值的符号确定单调区间. 当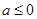 时,
时,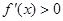 ,所以
,所以 的单调增区间为
的单调增区间为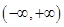 .当
.当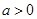 时,令
时,令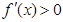 ,得
,得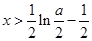 ,所以
,所以 的单调增区间是
的单调增区间是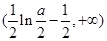 ;令
;令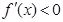 ,得
,得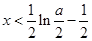 ,所以
,所以 的单调减区间是
的单调减区间是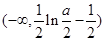 .(Ⅲ)不等式恒成立问题,一般利用变量分离转化为最值问题. “当
.(Ⅲ)不等式恒成立问题,一般利用变量分离转化为最值问题. “当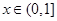 时,
时,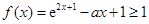 恒成立”
恒成立”等价于“当
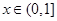 时,
时,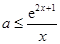 恒成立.”设
恒成立.”设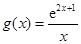 ,只要“当
,只要“当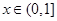 时,
时,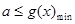 成立.”
成立.”易得函数
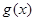 在
在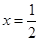 处取得最小值,所以实数
处取得最小值,所以实数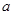 的取值范围
的取值范围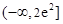 .
.(Ⅰ)由已知得
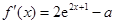 .
.因为曲线
 在点
在点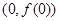 处的切线与直线
处的切线与直线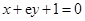 垂直,
垂直,所以
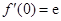 .所以
.所以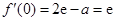 .
.所以
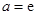 . 3分
. 3分(Ⅱ)函数
 的定义域是
的定义域是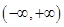 ,
,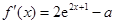 .
. (1)当
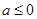 时,
时,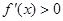 成立,所以
成立,所以 的单调增区间为
的单调增区间为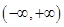 .
. (2)当
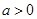 时,
时,令
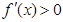 ,得
,得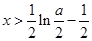 ,所以
,所以 的单调增区间是
的单调增区间是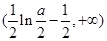 ;
;令
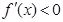 ,得
,得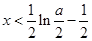 ,所以
,所以 的单调减区间是
的单调减区间是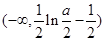 .
. 综上所述,当
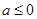 时,
时, 的单调增区间为
的单调增区间为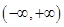 ;
;当
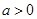 时,
时, 的单调增区间是
的单调增区间是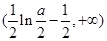 ,
, 的单调减区间是
的单调减区间是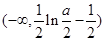 . 8分
. 8分(Ⅲ)当
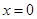 时,
时,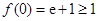 成立,
成立,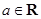 .
. “当
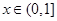 时,
时,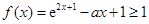 恒成立”
恒成立”等价于“当
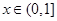 时,
时,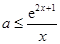 恒成立.”
恒成立.”设
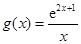 ,只要“当
,只要“当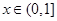 时,
时,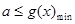 成立.”
成立.”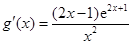 .
.令
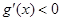 得,
得,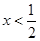 且
且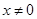 ,又因为
,又因为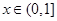 ,所以函数
,所以函数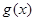 在
在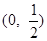 上为减函数;
上为减函数; 令
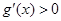 得,
得,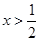 ,又因为
,又因为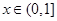 ,所以函数
,所以函数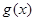 在
在 上为增函数.
上为增函数. 所以函数
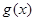 在
在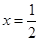 处取得最小值,且
处取得最小值,且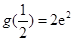 .
.所以
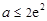 . 又因为
. 又因为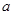
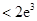 ,
,所以实数
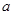 的取值范围
的取值范围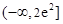 . 13分
. 13分(Ⅲ)另解:
(1)当
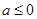 时,由(Ⅱ)可知,
时,由(Ⅱ)可知,  在
在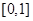 上单调递增,所以
上单调递增,所以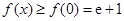 .
.所以当
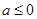 时,有
时,有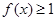 成立.
成立.(2)当
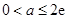 时, 可得
时, 可得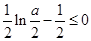 .
.由(Ⅱ)可知当
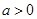 时,
时, 的单调增区间是
的单调增区间是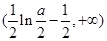 ,
,所以
 在
在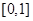 上单调递增,又
上单调递增,又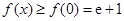 ,所以总有
,所以总有 成立.
成立.(3)当
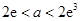 时,可得
时,可得 .
.由(Ⅱ)可知,函数
 在
在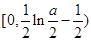 上为减函数,在
上为减函数,在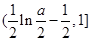 为增函数,
为增函数,所以函数
 在
在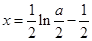 处取最小值,
处取最小值,且
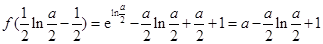 .
.当
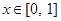 时,要使
时,要使 成立,只需
成立,只需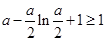 ,
,解得
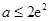 .所以
.所以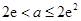 .
.综上所述,实数
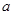 的取值范围
的取值范围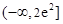 .
.
练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
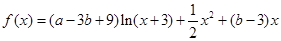 .
.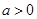 且
且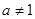 ,
,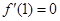 时,试用含
时,试用含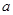 的式子表示
的式子表示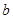 ,并讨论
,并讨论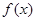 的单调区间;
的单调区间;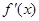 有零点,
有零点,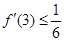 ,且对函数定义域内一切满足
,且对函数定义域内一切满足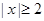 的实数
的实数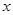 有
有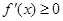 .
.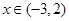 时,求函数
时,求函数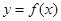 的图像与函数
的图像与函数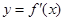 的图像的交点坐标.
的图像的交点坐标.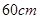 的正方形铁皮的四切去相等的正方形,再把它的边沿虚线折起,做成一个无盖的方底箱子,箱底的边长是多少时,箱子的容积最大?最大容积是多少?
的正方形铁皮的四切去相等的正方形,再把它的边沿虚线折起,做成一个无盖的方底箱子,箱底的边长是多少时,箱子的容积最大?最大容积是多少?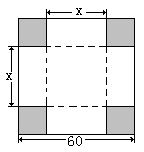
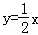 +2,
+2,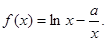
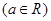
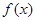 的单调增区间;
的单调增区间;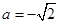 ,求函数
,求函数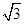 ,那么当该棱锥的体积最大时,它的高为( )
,那么当该棱锥的体积最大时,它的高为( )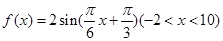 的图像与
的图像与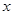 轴交于点
轴交于点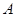 ,过点
,过点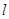 与函数
与函数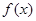 的图像交于
的图像交于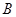
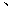
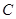 两点,则
两点,则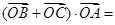 ( )
( )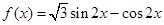 (
(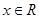 ).
).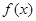 的单调递增区间;
的单调递增区间;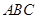 中,
中,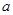 、
、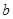 、
、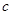 分别是角
分别是角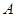 、
、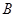 、
、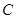 的对边,若
的对边,若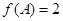 ,
,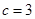 ,
,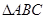 的面积为
的面积为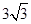 ,求
,求