题目内容
已知等差数列{an}中,a2+a4=10,a5=9,数列{bn}中,b1=a1,bn+1=bn+an.
(1)求数列{an}的通项公式,写出它的前n项和Sn.
(2)求数列{bn}的通项公式.
(3)若cn=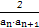 ,求数列{cn}的前n项和Tn.
,求数列{cn}的前n项和Tn.
(1)求数列{an}的通项公式,写出它的前n项和Sn.
(2)求数列{bn}的通项公式.
(3)若cn=
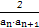 ,求数列{cn}的前n项和Tn.
,求数列{cn}的前n项和Tn.(1) an=2n-1,Sn= n2 (2) bn=n2-2n+2 (3) Tn= =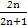
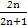
(1)设{an}的公差为d,由题意得a1=1,d=2,
所以an=2n-1,Sn=na1+ d=n2.
d=n2.
(2)b1=a1=1,bn+1=bn+an=bn+2n-1,
所以b2=b1+1,b3=b2+3=b1+1+3,
bn=b1+1+3+…+(2n-3)=1+(n-1)2=n2-2n+2(n≥2).
又n=1时n2-2n+2=1=b1,
所以数列{bn}的通项公式为bn=n2-2n+2.
(3)cn=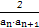 =
=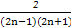 =
=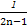 -
- ,
,
Tn=c1+c2+…+cn=( -
- )+(
)+( -
- )+…+(
)+…+(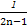 -
- )=1-
)=1- =
=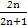 .
.
所以an=2n-1,Sn=na1+
 d=n2.
d=n2.(2)b1=a1=1,bn+1=bn+an=bn+2n-1,
所以b2=b1+1,b3=b2+3=b1+1+3,
bn=b1+1+3+…+(2n-3)=1+(n-1)2=n2-2n+2(n≥2).
又n=1时n2-2n+2=1=b1,
所以数列{bn}的通项公式为bn=n2-2n+2.
(3)cn=
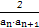 =
=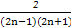 =
=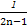 -
- ,
,Tn=c1+c2+…+cn=(
 -
- )+(
)+( -
- )+…+(
)+…+(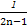 -
- )=1-
)=1- =
=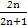 .
.
练习册系列答案
相关题目
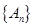 满足
满足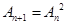 ,则称数列
,则称数列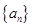 中,
中,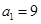 ,点
,点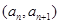 在函数
在函数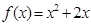 的图象上,其中
的图象上,其中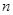 为正整数.
为正整数.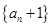 是“平方递推数列”,且数列
是“平方递推数列”,且数列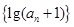 为等比数列;
为等比数列;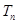 ,
,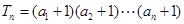 ,求
,求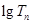 ;
;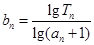 ,求数列
,求数列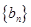 的前
的前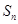 ,并求使
,并求使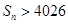 的
的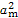 =0,S2m-1=38,则m=( )
=0,S2m-1=38,则m=( ) +
+ ),a3+a4+a5=64(
),a3+a4+a5=64( +
+ ),
),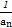 )2,求数列{bn}的前n项和Tn.
)2,求数列{bn}的前n项和Tn.
 中,
中,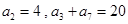 ,则
,则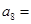 ( )
( )