题目内容
若实数x、y、m满足|x-m|>|y-m|,则称x比y远离m,
(Ⅰ)若x2-1比1远离0,求x的取值范围;
(Ⅱ)对任意两个不相等的正数a、b,证明:a3+b3比a2b+ab2远离2ab ;
;
(Ⅲ)已知函数f(x)的定义域D={x|x≠ ,k∈Z,x∈R},任取x∈D,f(x)等于sinx和cosx中远离0的那个值.写出函数f(x)的解析式,并指出它的基本性质(结论不要求证明).
,k∈Z,x∈R},任取x∈D,f(x)等于sinx和cosx中远离0的那个值.写出函数f(x)的解析式,并指出它的基本性质(结论不要求证明).
(Ⅰ)若x2-1比1远离0,求x的取值范围;
(Ⅱ)对任意两个不相等的正数a、b,证明:a3+b3比a2b+ab2远离2ab
 ;
;(Ⅲ)已知函数f(x)的定义域D={x|x≠
 ,k∈Z,x∈R},任取x∈D,f(x)等于sinx和cosx中远离0的那个值.写出函数f(x)的解析式,并指出它的基本性质(结论不要求证明).
,k∈Z,x∈R},任取x∈D,f(x)等于sinx和cosx中远离0的那个值.写出函数f(x)的解析式,并指出它的基本性质(结论不要求证明). (Ⅰ)解:由题意得|x2-1|>1,x2-1<-1或x2-1>1,即x2<0或x2>2,
∴x的取值范围是(-∞,-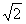 )∪(
)∪(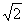 ,+∞)。
,+∞)。
(Ⅱ)证明:当a、b是不相等的正数时,
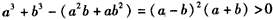 ,
,
又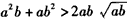 ,
,
则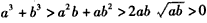 ,
,
于是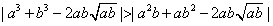 ,
,
∴a3+b3比a2b+ab2远离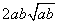 。
。
(Ⅲ)解:若|sinx|>|cosx| ,即sin2x>cos2x,cos2x<0,
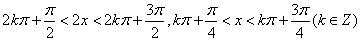 ;
;
同理,若|cosx|>|sinx|,则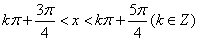 ,
,
于是,函数f(x)的解析式是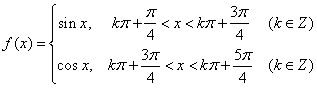 ,
,
函数f(x)的大致图象如下:

函数f(x)的最小正周期T=2π,函数f(x)是非奇非偶函数;
当x=2kπ或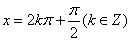 时,函数f(x)取得最大值1;
时,函数f(x)取得最大值1;
当x=2kπ+π或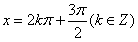 时,函数f(x)取得最小值-1;
时,函数f(x)取得最小值-1;
函数f(x)在区间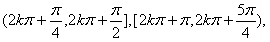
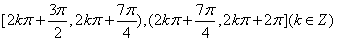 上单调递增;
上单调递增;
在区间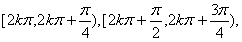
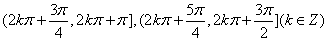 上单调递减。
上单调递减。
∴x的取值范围是(-∞,-
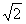 )∪(
)∪(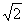 ,+∞)。
,+∞)。(Ⅱ)证明:当a、b是不相等的正数时,
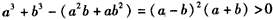 ,
,又
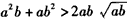 ,
,则
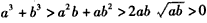 ,
,于是
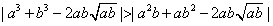 ,
,∴a3+b3比a2b+ab2远离
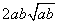 。
。(Ⅲ)解:若|sinx|>|cosx| ,即sin2x>cos2x,cos2x<0,
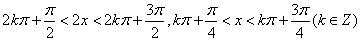 ;
;同理,若|cosx|>|sinx|,则
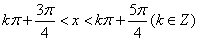 ,
,于是,函数f(x)的解析式是
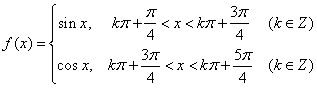 ,
,函数f(x)的大致图象如下:

函数f(x)的最小正周期T=2π,函数f(x)是非奇非偶函数;
当x=2kπ或
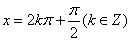 时,函数f(x)取得最大值1;
时,函数f(x)取得最大值1;当x=2kπ+π或
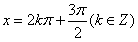 时,函数f(x)取得最小值-1;
时,函数f(x)取得最小值-1;函数f(x)在区间
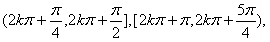
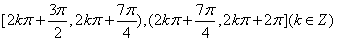 上单调递增;
上单调递增;在区间
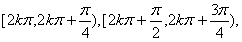
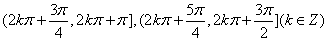 上单调递减。
上单调递减。 
练习册系列答案
相关题目