题目内容
(本小题满分10分)选修4-4:坐标系于参数方程
在直角坐标系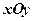 中,以O为极点,x正半轴为极轴建立极坐标系,曲线
中,以O为极点,x正半轴为极轴建立极坐标系,曲线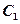 的极坐标方程为
的极坐标方程为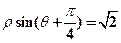 ,M,N分别为
,M,N分别为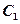 与x轴,y轴的交点。曲线
与x轴,y轴的交点。曲线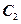 的参数方程为
的参数方程为
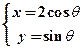 (
(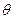 为参数)。
为参数)。
(Ⅰ)求M,N的极坐标,并写出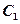 的直角坐标方程;
的直角坐标方程;
(Ⅱ)求N点与曲线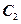 上的动点距离的最大值。
上的动点距离的最大值。
在直角坐标系
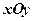 中,以O为极点,x正半轴为极轴建立极坐标系,曲线
中,以O为极点,x正半轴为极轴建立极坐标系,曲线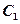 的极坐标方程为
的极坐标方程为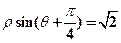 ,M,N分别为
,M,N分别为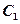 与x轴,y轴的交点。曲线
与x轴,y轴的交点。曲线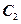 的参数方程为
的参数方程为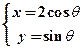 (
(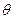 为参数)。
为参数)。(Ⅰ)求M,N的极坐标,并写出
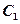 的直角坐标方程;
的直角坐标方程;(Ⅱ)求N点与曲线
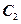 上的动点距离的最大值。
上的动点距离的最大值。(Ⅰ)
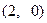 ;
;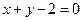
(Ⅱ)
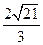
解:(Ⅰ)当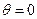 时,
时,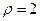 ,所以
,所以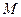 点的极坐标为
点的极坐标为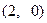
当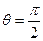 时,
时,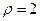 ,所以
,所以 点的极坐标为
点的极坐标为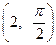 。
。
由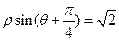 ,可得
,可得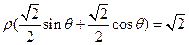 ,
,
因为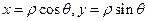 ,所以有
,所以有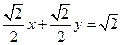
所以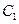 的直角坐标方程为
的直角坐标方程为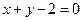 。
。
(Ⅱ)设曲线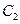 上的动点为
上的动点为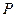 ,则
,则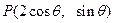 ,
,
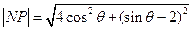
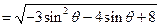
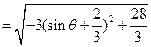
当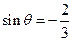 时
时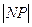 的最大值为
的最大值为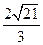 ,故
,故 点与曲线
点与曲线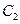 上的动点距离的最大值为
上的动点距离的最大值为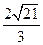 。
。
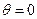 时,
时,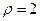 ,所以
,所以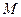 点的极坐标为
点的极坐标为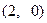
当
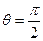 时,
时,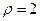 ,所以
,所以 点的极坐标为
点的极坐标为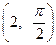 。
。由
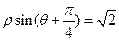 ,可得
,可得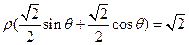 ,
,因为
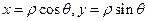 ,所以有
,所以有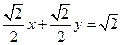
所以
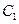 的直角坐标方程为
的直角坐标方程为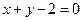 。
。(Ⅱ)设曲线
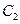 上的动点为
上的动点为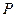 ,则
,则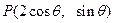 ,
,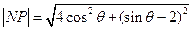
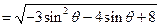
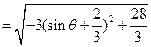
当
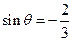 时
时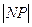 的最大值为
的最大值为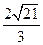 ,故
,故 点与曲线
点与曲线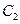 上的动点距离的最大值为
上的动点距离的最大值为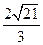 。
。
练习册系列答案
相关题目
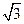 ,曲线段DE上任一点到A、B两点的距离之和都相等.
,曲线段DE上任一点到A、B两点的距离之和都相等.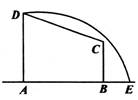
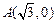 ,
,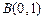 ,圆
,圆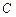 是以
是以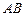 为直径的圆,直线
为直径的圆,直线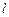 :
: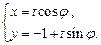 (
(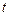 为参数).
为参数).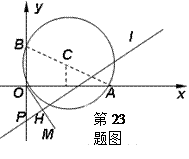
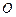 作直线
作直线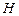 ,若动点
,若动点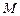 满足
满足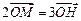 ,当
,当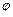 变化时,求点
变化时,求点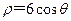 ,曲线C2的极坐标方程为
,曲线C2的极坐标方程为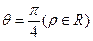 ,曲线C1,C2相交于点A,B.
,曲线C1,C2相交于点A,B.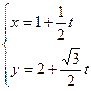 (t为参数);
(t为参数); 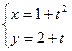 (t为参数);
(t为参数); 的方程为
的方程为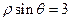 ,则点
,则点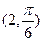 到直线
到直线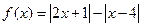 ,则不等式
,则不等式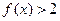 的解为
的解为 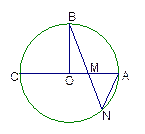 在极坐标系中,点
在极坐标系中,点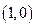 到直线
到直线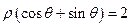 的距离为 .
的距离为 . 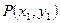 、
、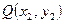 之间的“直角距离”为
之间的“直角距离”为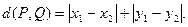 若
若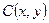 到点
到点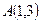 、
、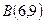 的“直角距离”相等,其中实
的“直角距离”相等,其中实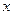 、
、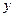 满足
满足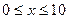 、
、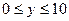 ,则所有满足条件的点
,则所有满足条件的点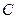 的轨迹的长度之和为( )
的轨迹的长度之和为( )


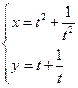 (t是参数,t≠0),它的普通方程是 .
(t是参数,t≠0),它的普通方程是 .