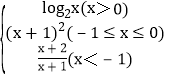题目内容
【题目】已知函数![]() 是
是![]() 上的奇函数.
上的奇函数.
(1)求![]() 的值;
的值;
(2)证明![]() 在
在![]() 上单调递减;
上单调递减;
(3)若对任意的![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)证明见解析;(3)
(2)证明见解析;(3)![]()
【解析】
(1)利用![]() 即可求解;
即可求解;
(2)利用函数单调性的定义证明即可;
(3)根据函数![]() 的单调性以及奇偶性,将不等式
的单调性以及奇偶性,将不等式![]() 化为
化为![]() ,再根据
,再根据![]() ,由二次函数的性质,求出实数
,由二次函数的性质,求出实数![]() 的取值范围.
的取值范围.
解:(1) 由函数![]() 是
是![]() 上的奇函数知道其图像必经过原点,
上的奇函数知道其图像必经过原点,
即必有![]() ,即
,即![]() ,解得
,解得![]()
(2)由(1)知![]() .任取
.任取![]() 且
且![]() ,则
,则
![]()
![]()
因为![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
又因为![]() 且
且![]() ,故
,故![]() ,
,
所以![]() ,即
,即![]()
所以![]() 在
在![]() 上单调递减
上单调递减
(3) 不等式![]() 可化为
可化为
![]()
因为![]() 是奇函数,故
是奇函数,故![]()
所以不等式又可化为![]()
由(2)知![]() 在
在![]() 上单调递减,故必有
上单调递减,故必有![]()
即![]()
因此知题设条件是:对任意的![]() ,不等式
,不等式![]() 恒成立
恒成立
设![]() ,则易知当
,则易知当![]() 时,
时,![]()
因此知当![]() 时,不等式
时,不等式![]() 恒成立
恒成立

 特高级教师点拨系列答案
特高级教师点拨系列答案【题目】在用二分法求方程![]() 在区间
在区间![]() 内的近似解时,先将方程变形为
内的近似解时,先将方程变形为![]() ,构建
,构建![]()
![]() ,然后通过计算以判断
,然后通过计算以判断![]() 及
及![]() 的正负号,再按步骤取区间中点值,计算中点的函数近似值,如此往复缩小零点所在区间,计算得部分数据列表如下:
的正负号,再按步骤取区间中点值,计算中点的函数近似值,如此往复缩小零点所在区间,计算得部分数据列表如下:
步骤 | 区间左端点 | 区间右端点 |
| 中点 |
1 | 2 | 3 | 2.5 | -0.102 |
2 | 0.189 | |||
3 | 2.625 | 0.044 | ||
4 | 2.5 | 2.625 | 2.5625 | -0.029 |
5 | 2.5625 | 2.625 | 2.59375 | 0.008 |
6 | 2.5625 | 2.59375 | 2.578125 | -0.011 |
7 | 2.578125 | 2.59375 | 2.5859375 | -0.001 |
8 | 2.5859375 | 2.59375 | 2.58984375 | 0.003 |
9 | 2.5859375 | 2.58984375 | 2.587890625 | 0.001 |
(1)判断![]() 及
及![]() 的正负号;
的正负号;
(2)请完成上述表格,在空白处填上正确的数字;
(3)若给定的精确度为0.1,则到第几步骤即可求出近似值?此时近似值为多少?
(4)若给定的精确度为0.01,则需要到第几步骤才可求出近似值?近似值为多少?