Question

【题目】定长为2的线段AB的两个端点在以点（0， ）为焦点的抛物线x2=2py上移动，记线段AB的中点为M，求点M到x轴的最短距离，并求此时点M的坐标。

Answer 1

【答案】最短距离为,（， ）

【解析】试题分析：由题意得到抛物线的方程，设直线的方程，联立方程组，得到和，根据，求得，进而利用基本不等式，即可求解的最小值，得到此时点的坐标.

试题解析：

依题意可得抛物线的方程为x2=y.

设直线AB的方程为y=kx+b（kR），

联立方程组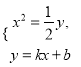得2x2-kx-b=0.

设A（x1,y1），B（x2，y2），则x1+x2=,x1x2=-,y1+y2=.

因为|AB|=2,所以（1+k2）[（x1+x2）2-4x1x2]=4，

所以b=，

所以yM=

=.

当且仅当=即k=±时取等号，

所以点M到x轴的最短距离为，此时点M的坐标为（， ）.