题目内容
【题目】已知圆C1:(x+1)2+y2=25,圆C2:(x﹣1)2+y2=1,动圆C与圆C1和圆C2均内切. 
(1)求动圆圆心C的轨迹E的方程;
(2)点P(1,t)为轨迹E上点,且点P为第一象限点,过点P作两条直线与轨迹E交于A,B两点,直线PA,PB斜率互为相反数,则直线AB斜率是否为定值,若是,求出定值;若不是,请说明理由.
【答案】
(1)解:圆C1:(x+1)2+y2=25的圆心C1(﹣1,0),半径r1=5;圆C2:(x﹣1)2+y2=1的圆心C2(1,0),半径r2=1.
设动圆C的圆心C(x,y),半径r.
∵动圆C与圆C1,圆C2均内切,
∴|C1C|=5﹣r,|C2C|=r﹣1.
∴|C1C|+|C2C|=5﹣1=4>|C1C2|=2,
因此动点C的轨迹是椭圆,且2a=4,2c=2,得a=2,c=1,
∴b2=a2﹣c2=3.
因此动圆圆心C的轨迹E方程是 ![]() ;
;
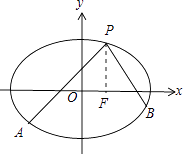
(2)解:如图,
∵点P(1,t)为轨迹E上点,且点P为第一象限点,
∴ ![]() ,解得t=
,解得t= ![]() ,
,
∴P(1, ![]() ),
),
设PA所在直线方程为y﹣ ![]() ,则PB所在直线方程为
,则PB所在直线方程为 ![]() ,
,
联立 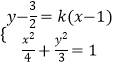 ,得(3+4k2)x2﹣(8k2﹣12k)x+4k2﹣12k﹣3=0,
,得(3+4k2)x2﹣(8k2﹣12k)x+4k2﹣12k﹣3=0,
则 ![]() ,
,
∴ ![]() ,
, ![]() ,
,
取k为﹣k,可得 ![]() ,
,
∴ 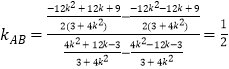 .
.
∴直线AB斜率为定值 ![]() .
.
【解析】(1)圆(x+1)2+y2=1的圆心C1(﹣1,0),半径r1=1;圆(x﹣1)2+y2=25的圆心C2(1,0),半径r2=5.设动圆C的圆心C(x,y),半径r.由于动圆C与圆(x+1)2+y2=1及圆(x﹣1)2+y2=25都内切,可得|C1C|=r﹣1,|C2C|=5﹣r.于是|C1C|+|C2C|=5﹣1=4>|C1C2|=2,利用椭圆的定义可知:动点C的轨迹是椭圆;(2)把P的坐标代入椭圆方程,求得t值,然后设出过PA的直线方程,PB的直线方程,联立直线方程和椭圆方程,求得A,B的坐标,代入斜率公式可得直线AB斜率为定值 ![]() .
.