题目内容
【题目】如图所示,在Rt△ABC中,已知点A(-2,0),直角顶点B(0,-2![]() ),点C在x轴上。
),点C在x轴上。
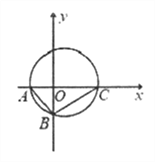
(1)求Rt△ABC外接圆的方程;
(2)求过点(-4,0)且与Rt△ABC外接圆相切的直线的方程。
【答案】(1) (x-1)2+y2=9 (2) 3x-4y+12=0或3x+4y+12=0
【解析】试题分析:(1)由题意得![]() ,得
,得![]() ,求得
,求得![]() ,进而得到圆的圆心坐标和半径,求得圆的方程;
,进而得到圆的圆心坐标和半径,求得圆的方程;
(2)设直线的方程为![]() ,根据直线与圆相切,圆心到直线的距离等于半径,求得
,根据直线与圆相切,圆心到直线的距离等于半径,求得![]() 的值,进而得到所求直线的方程.
的值,进而得到所求直线的方程.
试题解析:
(1)设点C(a,0),由AB⊥BC可得kAB·kBC=-1,即![]() ·
·![]() =-1,解得a=4.
=-1,解得a=4.
则所求的圆的圆心为AC的中点(1,0),半径为3,
所求圆的方程为(x-1)2+y2=9.
(2)由题意知直线的斜率存在,设所求直线的方程为y=k(x+4),即kx-y+4k=0.
当直线和圆相切时,圆心到直线的距离等于半径,所以![]() =3,解得k=
=3,解得k=![]()
![]() ,
,
所求直线的方程为y=![]() (x+4)或y=-
(x+4)或y=-![]() (x+4),
(x+4),
即3x-4y+12=0或3x+4y+12=0.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目