题目内容
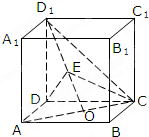 如图:在正方体ABCD-A1B1C1D1中,O、O1分别是AC、A1C1的中点,E是线段D1O上一点,且D1E=λEO(λ≠0).
如图:在正方体ABCD-A1B1C1D1中,O、O1分别是AC、A1C1的中点,E是线段D1O上一点,且D1E=λEO(λ≠0).(Ⅰ)求证:λ取不等于0的任何值时都有BO1∥平面ACE;
(Ⅱ)λ=2时,证明:平面CDE⊥平面CD1O.
分析:(I)证明四边形D1O1BO是平行四边形,可得BO1∥OE,利用线面平行的判定定理,可得结论;
(II)求出平面CD1O的一个法向量、平面CDE的法向量,证明
•
=0,可得平面CDE⊥平面CD1O.
(II)求出平面CD1O的一个法向量、平面CDE的法向量,证明
| DB1 |
| n |
解答: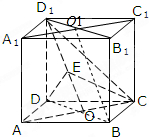 证明:(I)由题意,O、O1分别是AC、A1C1的中点,
证明:(I)由题意,O、O1分别是AC、A1C1的中点,
∴四边形D1O1BO是平行四边形,
∴BO1∥OD1
∴BO1∥OE
∵OE?平面ACE,BO1?平面ACE,
∴λ取不等于0的任何值时都有BO1∥平面ACE;
(Ⅱ) 不妨设正方体的棱长为1,以DA,DC,DD1为x,y,z轴建立空间直角坐标系,
不妨设正方体的棱长为1,以DA,DC,DD1为x,y,z轴建立空间直角坐标系,
则可得D(0,0,0),B1(1,1,1),O(
,
,0),C(0,1,0),D1(0,0,1)
∴
=(1,1,1),
=(0,-1,1),
=(-
,
,0)
∴
•
=0,
•
=0
∴DB1⊥CD1,DB1⊥OC
∴平面CD1O的一个法向量为
=(1,1,1),
∵λ=2,∴E(
,
,
)
又设平面CDE的法向量为
=(x,y,z)
∵
=(0,1,0),
=(
,
,
)
∴
∴可取
=(1,0,-1)
∴
•
=0
∴平面CDE⊥平面CD1O.
 证明:(I)由题意,O、O1分别是AC、A1C1的中点,
证明:(I)由题意,O、O1分别是AC、A1C1的中点,∴四边形D1O1BO是平行四边形,
∴BO1∥OD1
∴BO1∥OE
∵OE?平面ACE,BO1?平面ACE,
∴λ取不等于0的任何值时都有BO1∥平面ACE;
(Ⅱ)
 不妨设正方体的棱长为1,以DA,DC,DD1为x,y,z轴建立空间直角坐标系,
不妨设正方体的棱长为1,以DA,DC,DD1为x,y,z轴建立空间直角坐标系,则可得D(0,0,0),B1(1,1,1),O(
| 1 |
| 2 |
| 1 |
| 2 |
∴
| DB1 |
| CD1 |
| OC |
| 1 |
| 2 |
| 1 |
| 2 |
∴
| DB1 |
| CD1 |
| DB1 |
| OC |
∴DB1⊥CD1,DB1⊥OC
∴平面CD1O的一个法向量为
| DB1 |
∵λ=2,∴E(
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
又设平面CDE的法向量为
| n |
∵
| DC |
| DE |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
∴
|
∴可取
| n |
∴
| DB1 |
| n |
∴平面CDE⊥平面CD1O.
点评:本题在正方体中研究线面平行和面面垂直的问题,考查了利用空间坐标系研究空间的垂直问题等知识点,属于中档题.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
 若Rt△ABC中两直角边为a、b,斜边c上的高为h,则
若Rt△ABC中两直角边为a、b,斜边c上的高为h,则 如图,在正方体的一角上截取三棱锥P-ABC,PO为棱锥的高,记
如图,在正方体的一角上截取三棱锥P-ABC,PO为棱锥的高,记 若Rt△ABC中两直角边为a、b,斜边c上的高为h,则
若Rt△ABC中两直角边为a、b,斜边c上的高为h,则 如图,在正方体ABCD-A1B1C1D1中,E为DD1的中点,
如图,在正方体ABCD-A1B1C1D1中,E为DD1的中点, 如图,在正方体ABCD-A1B1C1D1中,点P是上底面A1B1C1D1内一动点,则三棱锥P-ABC的主视图与左视图的面积的比值为( )
如图,在正方体ABCD-A1B1C1D1中,点P是上底面A1B1C1D1内一动点,则三棱锥P-ABC的主视图与左视图的面积的比值为( )