题目内容
如果对定义在 上的函数
上的函数 ,对任意两个不相等的实数
,对任意两个不相等的实数 ,都有
,都有 ,则称函数
,则称函数 为“
为“ 函数”.给出下列函数①
函数”.给出下列函数① ;②
;② ;③
;③ ;④
;④ .
.
以上函数是“ 函数”的所有序号为 .
函数”的所有序号为 .
②③
解析试题分析: 即
即 ,
,
所以函数 在
在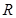 是增函数.
是增函数.
对于①,由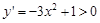 得
得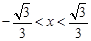 ,即函数在区间
,即函数在区间 是增函数,其不是“
是增函数,其不是“ 函数”;
函数”;
对于②,由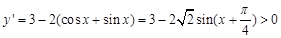 恒成立,所以其为“
恒成立,所以其为“ 函数”;
函数”;
对于③,由 恒成立,所以其为“
恒成立,所以其为“ 函数”;
函数”;
对于④,由于其为偶函数,所以其不可能在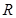 是增函数.所以不是“
是增函数.所以不是“ 函数”.
函数”.
综上知,是“ 函数”的有②③.
函数”的有②③.
考点:函数的单调性,应用导数研究函数的单调性.

练习册系列答案
相关题目

 ,若关于
,若关于 的方程
的方程 有三个不同的实根,则实数
有三个不同的实根,则实数 的取值范围是.
的取值范围是. 满足:
满足: ,则函数
,则函数 上的最小值为 .
上的最小值为 .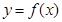 的定义域为
的定义域为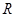 ,若存在常数
,若存在常数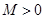 ,使
,使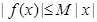 对一切
对一切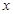 均成立,则称为“有界泛函”.现在给出如下
均成立,则称为“有界泛函”.现在给出如下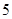 个函数:
个函数: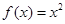 ; ②
; ②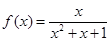 ;③
;③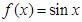 ;④
;④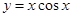 ;
;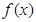 是
是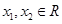 ,均有
,均有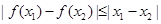 .
.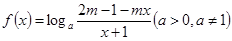 是奇函数,则函数
是奇函数,则函数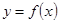 的定义域为
的定义域为  ,则函数
,则函数 的零点个数为 个.
的零点个数为 个. a)≤2f(1),则a的取值范围是________.
a)≤2f(1),则a的取值范围是________.