题目内容
设函数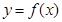 的定义域为
的定义域为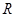 ,若存在常数
,若存在常数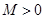 ,使
,使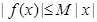 对一切
对一切
实数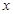 均成立,则称为“有界泛函”.现在给出如下
均成立,则称为“有界泛函”.现在给出如下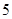 个函数:
个函数:
①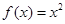 ; ②
; ②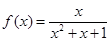 ;③
;③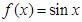 ;④
;④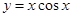 ;
;
⑤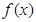 是
是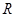 上的奇函数,且满足对一切
上的奇函数,且满足对一切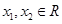 ,均有
,均有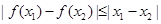 .
.
其中属于“有界泛函”的函数是 (填上所有正确的序号)
②③④⑤
解析试题分析:根据题意,要满足“有界泛函”的定义,必须存在常数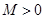 ,使得
,使得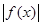 的图像不在
的图像不在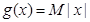 的图像的上方,我们结合定义及函数解析式或图象特征来判断.
的图像的上方,我们结合定义及函数解析式或图象特征来判断.
对于①,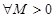 ,当
,当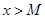 时
时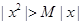 ,故不选①;
,故不选①;
对于②,函数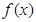 的定义域为
的定义域为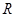 ,
,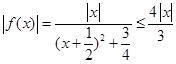 ,故②正确;
,故②正确;
对于③,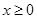 时由
时由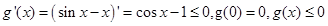 有
有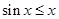 ,故
,故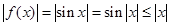 ,故③正确;
,故③正确;
对于④,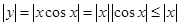 ,故④正确;
,故④正确;
对于⑤,令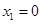 ,则
,则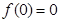 ,已知式化为
,已知式化为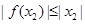 ,显然也符合定义.
,显然也符合定义.
考点:1、函数的定义;2、函数的图像与最值.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
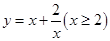 的值域是____________.
的值域是____________. 在区间
在区间 上单调递增,则
上单调递增,则 的取值范围是___________.
的取值范围是___________. ,若
,若 为奇函数,则
为奇函数,则 .
.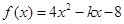 在区间
在区间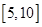 上具有单调性,则实数
上具有单调性,则实数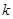 的取值范围是 .
的取值范围是 . 上的函数
上的函数 ,对任意两个不相等的实数
,对任意两个不相等的实数 ,都有
,都有 ,则称函数
,则称函数 函数”.给出下列函数①
函数”.给出下列函数① ;②
;② ;③
;③ ;④
;④ .
.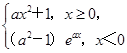 在(-∞,+∞)上单调,则a的取值范围是________.
在(-∞,+∞)上单调,则a的取值范围是________.