题目内容
2.已知函数y=2sin(2x+$\frac{π}{3}$)+1(1)求最小正周期;
(2)求最值及相应x的集合;
(3)当x∈[0,$\frac{π}{2}$]时,求函数的最值及相应的x的值.
分析 (1)由题意和周期公式可得;
(2)当2x+$\frac{π}{3}$=2kπ+$\frac{π}{2}$时,函数取最大值3,易得此时相应x的集合,同理可得最小值和相应的x集合;
(3)由x的范围可得2x+$\frac{π}{3}$∈[$\frac{π}{3}$,$\frac{4π}{3}$],可得当2x+$\frac{π}{3}$=$\frac{π}{2}$即x=$\frac{π}{12}$时,函数取最大值3,当2x+$\frac{π}{3}$=$\frac{4π}{3}$即x=$\frac{π}{2}$时,函数取最小值1-$\sqrt{3}$.
解答 解:(1)由题意和周期公式可得函数的最小正周T=$\frac{2π}{2}$=π;
(2)当2x+$\frac{π}{3}$=2kπ+$\frac{π}{2}$时,函数取最大值3,此时相应x的集合为{x|x=kπ+$\frac{π}{12}$,k∈Z};
当2x+$\frac{π}{3}$=2kπ-$\frac{π}{2}$时,函数取最小值-1,此时相应x的集合为{x|x=kπ-$\frac{5π}{12}$,k∈Z};
(3)∵x∈[0,$\frac{π}{2}$],∴2x+$\frac{π}{3}$∈[$\frac{π}{3}$,$\frac{4π}{3}$],
∴当2x+$\frac{π}{3}$=$\frac{π}{2}$即x=$\frac{π}{12}$时,函数取最大值3,
当2x+$\frac{π}{3}$=$\frac{4π}{3}$即x=$\frac{π}{2}$时,函数取最小值1-$\sqrt{3}$.
点评 本题考查正弦函数的图象,涉及周期性和最值,属中档题.

练习册系列答案
相关题目
14.斜四棱柱的侧面是矩形的面最多有( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
12.已知直线l1:y=2x+1,${l_2}:y=-\frac{1}{2}x-2$则两条直线的位置关系为( )
| A. | 平行 | B. | 重合 | C. | 相交但不垂直 | D. | 垂直 |
 如图,修建一个面积为2$\sqrt{3}$m2的三角形花园,已知ABC中,∠A=120°,AC=2m,则AB的长为多少?
如图,修建一个面积为2$\sqrt{3}$m2的三角形花园,已知ABC中,∠A=120°,AC=2m,则AB的长为多少?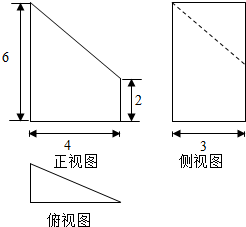 几何体的三视图如图所示,则该几何体的体积为28.
几何体的三视图如图所示,则该几何体的体积为28. 在直角三棱柱ABC-A1B1C1中,若BC⊥AC,∠BAC=$\frac{π}{3}$,AC=4,AA1=4,M为AA1中点,点P为BM中点,Q在线段CA1上,且A1Q=3QC,则PQ的长度为$\sqrt{13}$.
在直角三棱柱ABC-A1B1C1中,若BC⊥AC,∠BAC=$\frac{π}{3}$,AC=4,AA1=4,M为AA1中点,点P为BM中点,Q在线段CA1上,且A1Q=3QC,则PQ的长度为$\sqrt{13}$.