题目内容
【题目】已知过点A（﹣2，0）的直线与x=2相交于点C，过点B（2，0）的直线与x=﹣2相交于点D，若直线CD与圆x2+y2=4相切，则直线AC与BD的交点M的轨迹方程为 ．
【答案】
+y2=1（x≠±2）
【解析】解：设C（2，y1），D（﹣2，y2），则直线CD的方程为y﹣y1= 
（x﹣2），
即（y1﹣y2）x﹣4y+2（y1+y2）=0，
∵直线CD与圆x2+y2=4相切，
∴ 
=2，整理得y1y2=4．
设M（x0，y0），则直线AM的方程为y= 
（x+2），
令x=2得y= 
，即y1= ，
同理得y2= 
，
∵y1y2=4．
∴ =4，
即x02+4y02=4，即 
+y02=1．
∴M的轨迹方程为： 
=1（x≠±2）．
所以答案是： =1（x≠±2）．
练习册系列答案
期末1卷素质教育评估卷系列答案
相关题目
【题目】已知某产品的广告费用x（单位：万元）与销售额y（单位：万元）具有线性关系关系，其统计数据如下表：
x | 3 | 4 | 5 | 6 |
y | 25 | 30 | 40 | 45 |
由上表可得线性回归方程 
= 
x+ 
，据此模型预报广告费用为8万元时的销售额是（ ）
附： = 
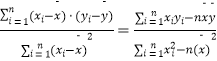； = ﹣ x．
A.59.5
B.52.5
C.56
D.63.5
