题目内容
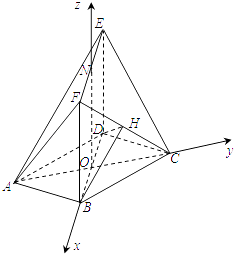
【题目】如图，在多面体ABCDEF中，底面ABCD是边长为2的菱形，∠BAD=60°，四边形BDEF是矩形，平面BDEF⊥平面ABCD，BF=3，H是CF的中点． 
（Ⅰ）求证：AC⊥平面BDEF；
（Ⅱ）求直线DH与平面BDEF所成角的正弦值；
（Ⅲ）求二面角H﹣BD﹣C的大小．
【答案】解：（Ⅰ）证明：∵四边形ABCD是菱形，
∴AC⊥BD．
又∵平面BDEF⊥平面ABCD，平面BDEF∩平面ABCD=BD，
且AC平面ABCD，
∴AC⊥平面BDEF；
（Ⅱ）解：设AC∩BD=O，取EF的中点N，连接ON，
∵四边形BDEF是矩形，O，N分别为BD，EF的中点，
∴ON∥ED，
∵ED⊥平面ABCD，
∴ON⊥平面ABCD，
由AC⊥BD，得OB，OC，ON两两垂直．
∴以O为原点，OB，OC，ON所在直线分别为x轴，y轴，z轴，如图建立空间直角坐标系．
∵底面ABCD是边长为2的菱形，∠BAD=60°，BF=3，
∴A（0，﹣ 
，0），B（1，0，0），D（﹣1，0，0），E（﹣1，0，3），F（1，0，3），C（0， ，0），H（ 
， 
， 
）
∵AC⊥平面BDEF，
∴平面BDEF的法向量 
=（0，2 ，0）．
设直线DH与平面BDEF所成角为α，
∵ 
=（ ， ， ），
∴sinα=|cos＜ ， ＞|=| 
|= 
，
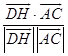∴直线DH与平面BDEF所成角的正弦值为 ；
（Ⅲ）解：由（Ⅱ），得 
=（﹣ ， ， ）， 
=（2，0，0）．
设平面BDH的法向量为 
=（x，y，z），则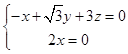 
令z=1，得 =（0，﹣ 
，1）
由ED⊥平面ABCD，得平面BCD的法向量为 
=（0，0，﹣3），
则cos＜ ， ＞= 
=﹣ ，
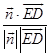由图可知二面角H﹣BD﹣C为锐角，
∴二面角H﹣BD﹣C的大小为60°．
【解析】（I）由面面垂直的性质可证AC与平面BDEF垂直；（Ⅱ）以O为原点，OB，OC，ON所在直线分别为x轴，y轴，z轴，建立空间直角坐标系，求出平面BDEF的法向量，即可求直线DH与平面BDEF所成角的正弦值；（Ⅲ）求出平面BDH、平面BCD的法向量，利用向量的夹角公式，即可求二面角H﹣BD﹣C的大小．
【考点精析】本题主要考查了空间角的异面直线所成的角的相关知识点，需要掌握已知
为两异面直线，A，C与B，D分别是上的任意两点，所成的角为
，则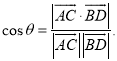
才能正确解答此题．
