题目内容
【题目】如图,四棱锥S﹣ABCD中,SD=CD=SC=2AB=2BC,平面ABCD⊥底面SDC,AB∥CD,∠ABC=90°,E是SD中点.
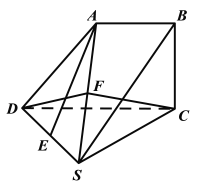
(1)证明:直线AE//平面SBC;
(2)点F为线段AS的中点,求二面角F﹣CD﹣S的大小.
【答案】(1)详见解析;(2)30°.
【解析】
(1)取SC中点G,连接BG,EG,推导出四边形AEGB为平行四边形,从而AE∥BG,进而AE∥平面SBC;
(2)取CD中点O,连接OS,OA ,推导出四边形ABCD为矩形,AO⊥CO,AO⊥CD,以O为原点,OS所在直线为x轴,OC所在直线为y轴,OA所在直线为z轴,建立空间直角坐标系,利用向量法能求出二面角F﹣CD﹣S的大小.
(1)证:如图,取SC中点G,连接BG,EG,
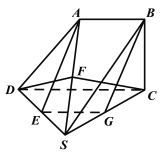
∵EG为△SDC的中位线,∴EG∥CD,且EG![]() ,
,
∵AB∥CD,且AB![]() ,∴EG∥CD,且EG=AB,
,∴EG∥CD,且EG=AB,
∴四边形AEGB为平行四边形,∴AE∥BG,
∵BG平面SBC,AE![]() 平面SBC,
平面SBC,
∴AE∥平面SBC;
(2)解:设AB=1,则BC=1,CD=2,取CD中点O,连接OS,OA ,
∴CO![]() ,
,
∵AB∥CD,∠ABC=90°,
∴四边形ABCO为矩形,∴AO⊥CO,AO⊥CD,
平面ABCD∩平面SDC=CD,∴AO⊥平面SDC,AO⊥SO,
∵△SDC为正三角形,∴SO⊥CD,
以O为原点,OS所在直线为x轴,OC所在直线为y轴,OA所在直线为z轴,建立如图所示的空间直角坐标系,
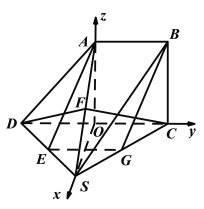
A(0,0,1),S(![]() ,0,0),C(0,1,0),D(0,﹣1,0),F(
,0,0),C(0,1,0),D(0,﹣1,0),F(![]() ,0,
,0,![]() ),
),
![]() (
(![]() ,1,
,1,![]() ),
),![]() (
(![]() ,﹣1,
,﹣1,![]() ),
),
设平面FCD的一个法向量![]() (a,b,c),
(a,b,c),
则 ,取x=1,得
,取x=1,得![]() (1,0,
(1,0,![]() ),
),
由题意取平面SDC的一个法向量![]() (0,0,1),
(0,0,1),
设二面角F﹣CD﹣S的大小为θ,
则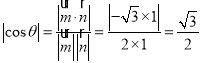 ,
,
由图可知,![]() 为锐角,∴θ=30°,
为锐角,∴θ=30°,
∴二面角F﹣CD﹣S的大小为30°.

 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案