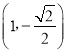题目内容
【题目】若存在a>0,使得函数f(x)=6a2lnx+4ax与g(x)=x2﹣b在这两函数图象的公共点处的切线相同,则b的最大值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】C
【解析】
设公共点为(x,y),然后根据公共点处函数值相等、导数值相等,列出关于公共点满足的方程组,将x消去,得到关于b,a的等量关系式,整理成b=h(a)的形式,求函数的最值即可.
设公共点为(x,y),(x>0),且![]() .
.
所以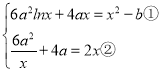 (a>0),由②得x2﹣2ax﹣3a2=0,
(a>0),由②得x2﹣2ax﹣3a2=0,
解得x=3a或﹣a(舍).
将x=3a代入①式整理得:b=﹣3a2﹣6a2ln(3a),(a>0),
令h(a)=﹣3a2﹣6a2ln(3a),(a>0),
∴![]() 12a[ln(3a)+1],
12a[ln(3a)+1],
令![]() =0得,
=0得,![]() ,且
,且![]() 时,
时,![]() <0.
<0.
故h(a)在(0,![]() )上递增,在(
)上递增,在(![]() )上递减.
)上递减.
故h(a)max=h(![]() )
)![]() .
.
故b的最大值为![]() .
.
故选:C.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
【题目】为了进一步激发同学们的学习热情,某班级建立了数学英语两个学习兴趣小组,两组的人数如下表所示:
组别 性别 | 数学 | 英语 |
男 | 5 | 1 |
女 | 3 | 3 |
现采用分层抽样的方法(层内采用简单随机抽样)从两组中共抽取3名同学进行测试.
(1)求从数学组抽取的同学中至少有1名女同学的概率;
(2)记ξ为抽取的3名同学中男同学的人数,求随机变量ξ的分布列和数学期望.