题目内容
【题目】已知函数f(x)=axex,g(x)=x2+2x+b,若曲线y=f(x)与曲线y=g(x)都过点P(1,c).且在点P处有相同的切线l.
(Ⅰ)求切线l的方程;
(Ⅱ)若关于x的不等式k[ef(x)]≥g(x)对任意x∈[﹣1,+∞)恒成立,求实数k的取值范围.
【答案】(Ⅰ)4x﹣y﹣2=0;(Ⅱ)![]() k≤e
k≤e
【解析】
(I)根据切点和斜率列方程,解方程组求得![]() 的值,进而求得切线方程.
的值,进而求得切线方程.
(II)构造函数![]() ,利用导数研究
,利用导数研究![]() 的单调性,对
的单调性,对![]() 进行分类讨论,结合
进行分类讨论,结合![]() 恒成立,由此求得
恒成立,由此求得![]() 的取值范围.
的取值范围.
(Ⅰ)∵f′(x)=aex(x+1),g′(x)=2x+2,由已知可得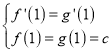 ,
,
即![]() ,解得a
,解得a![]() ,b=﹣1,c=2,∴切线的斜率g′(1)=4,
,b=﹣1,c=2,∴切线的斜率g′(1)=4,
∴切线l的方程为y﹣2=4(x﹣1),即4x﹣y﹣2=0,
(Ⅱ)由(Ⅰ)可得f(x)=2xex﹣1,g(x)=x2+2x﹣1,设h(x)=k[ef(x)]﹣g(x)=2kxex﹣(x2+2x﹣1),
即h(x)≥0,对任意x∈[﹣1,+∞)恒成立,从而h(x)min≥0,
∴h′(x)=2k(x+1)ex﹣2(x+1)=2(x+1)(kex﹣1),
①当k≤0时,h′(x)≤0,h(x)在[﹣1,+∞)上单调递减,又h(1)=2ke﹣2<0,显然h(x)≥0不恒成立,
②当k>0时,h′(x)=0,解得x1=﹣1,x2=﹣lnk,
(i)当﹣lnk<﹣1时,即k>e时,h′(x)≥0,h(x)单调递增,
又h(x)min=h(﹣1)![]() 2
2![]() 0,显然h(x)≥0不恒成立,
0,显然h(x)≥0不恒成立,
(ii)当﹣lnk=﹣1时,即k=e时,h′(x)>0,h(x)单调递增,
∴h(x)min=h(﹣1)![]() 2
2![]() 0,即h(x)≥0恒成立,
0,即h(x)≥0恒成立,
(iii)当﹣lnk>﹣1时,即0<k<e时,
当x∈[﹣1,﹣lnk)时,h′(x)<0,h(x)单调递减,当x∈(﹣lnk,+∞)时,h′(x)>0,h(x)单调递增,
∴h(x)min=h(﹣lnk)=-2lnk﹣(ln2k﹣2lnk﹣1)=1﹣ln2k≥0,解得![]() k≤e,∴
k≤e,∴![]() k<e,
k<e,
综上所述得:![]() k≤e.
k≤e.