题目内容
已知公差不为0的等差数列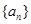 的前3项和
的前3项和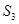 =9,且
=9,且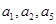 成等比数列
成等比数列
(1)求数列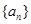 的通项公式和前n项和
的通项公式和前n项和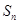 ;
;
(2)设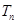 为数列
为数列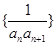 的前n项和,若
的前n项和,若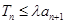 对一切
对一切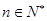 恒成立,求实数
恒成立,求实数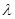 的最小值
的最小值
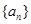 的前3项和
的前3项和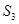 =9,且
=9,且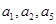 成等比数列
成等比数列 (1)求数列
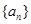 的通项公式和前n项和
的通项公式和前n项和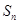 ;
;(2)设
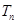 为数列
为数列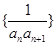 的前n项和,若
的前n项和,若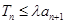 对一切
对一切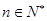 恒成立,求实数
恒成立,求实数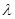 的最小值
的最小值 (1)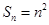 ;(2)实数
;(2)实数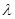 的最小值为
的最小值为
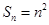 ;(2)实数
;(2)实数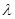 的最小值为
的最小值为
试题分析:(1)求数列
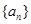 的通项公式和前n项和
的通项公式和前n项和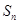 ,因为数列
,因为数列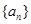 是公差不为0的等差数列,故只需求出
是公差不为0的等差数列,故只需求出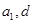 即可,由题意
即可,由题意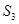 =9,且
=9,且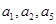 成等比数列,可得
成等比数列,可得 ,即
,即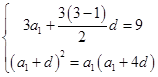 ,解出
,解出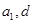 ,代入
,代入 ,可求出数列
,可求出数列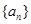 的通项公式和前n项和
的通项公式和前n项和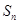 ;(2)求实数
;(2)求实数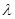 的最小值,由题意
的最小值,由题意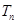 为数列
为数列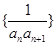 的前n项和,若
的前n项和,若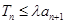 对一切
对一切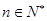 恒成立,关键是求数列
恒成立,关键是求数列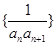 的通项公式,由(1)可知
的通项公式,由(1)可知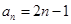 ,可得
,可得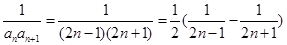 ,从而可得
,从而可得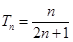 ,代入
,代入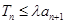 ,利用基本不等式,即可求出实数
,利用基本不等式,即可求出实数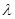 的最小值
的最小值 试题解析:(1)设
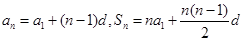 ,
,由
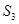 =9得:
=9得: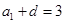 ①; 2分
①; 2分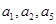 成等比数列得:
成等比数列得: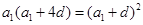 ②;联立①②得
②;联立①②得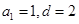 ; 4分
; 4分故
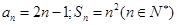 6分
6分(2)∵
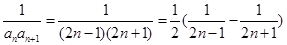 8分
8分∴
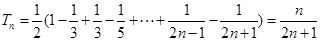 10分
10分由
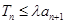 得:
得: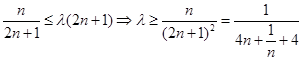
令
 ,可知f(n)单调递减,即
,可知f(n)单调递减,即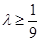 12分
12分
练习册系列答案
相关题目
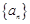 中,
中,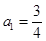 ,
,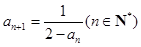 .
.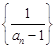 是等差数列,并求
是等差数列,并求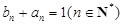 ,
,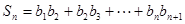 ,试比较
,试比较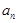 与
与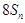 的大小.
的大小.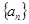 前n项和
前n项和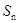 =
=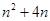 (
(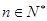 ), 数列
), 数列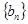 为等比数列,首项
为等比数列,首项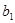 =2,公比为q(q>0)且满足
=2,公比为q(q>0)且满足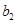 ,
,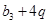 ,
,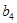 为等比数列.
为等比数列.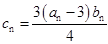 ,记数列
,记数列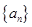 是公比为正数的等比数列,
是公比为正数的等比数列,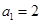 ,
,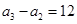 .
.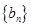 满足:
满足: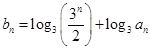 ,求数列
,求数列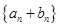 的前
的前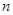 项和
项和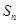 .
.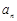 ,则
,则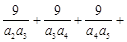 …
… =
= 
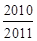
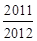
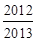
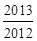
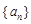 中,当
中,当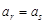
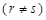 时,
时,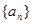 中,若
中,若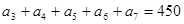 ,则数列
,则数列