题目内容
已知数列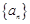 中,
中,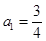 ,
,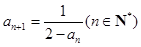 .
.
(1)求证:数列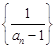 是等差数列,并求
是等差数列,并求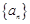 的通项公式;
的通项公式;
(2)设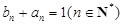 ,
,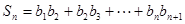 ,试比较
,试比较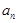 与
与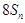 的大小.
的大小.
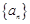 中,
中,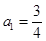 ,
,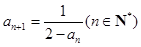 .
.(1)求证:数列
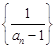 是等差数列,并求
是等差数列,并求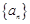 的通项公式;
的通项公式;(2)设
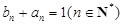 ,
,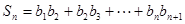 ,试比较
,试比较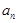 与
与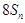 的大小.
的大小.(1)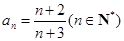 ;(2) 当
;(2) 当 时,
时,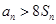 ;当
;当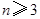 时,
时, .
.
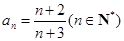 ;(2) 当
;(2) 当 时,
时,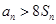 ;当
;当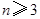 时,
时, .
.试题分析:(1)要证
 是等差数列,按照等差数列的定义,即证:
是等差数列,按照等差数列的定义,即证: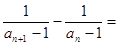 常数;由
常数;由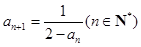 代入化简得到,
代入化简得到, 是等差数列,
是等差数列,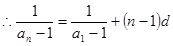 ,然后反解出
,然后反解出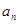 的通项公式;(2)由
的通项公式;(2)由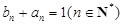 ,
,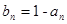 ,再计算
,再计算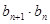 ,先将其裂项,由其形式确定用累加法求
,先将其裂项,由其形式确定用累加法求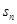 ,用做差比较
,用做差比较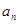 与
与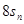 的大小,注意讨论
的大小,注意讨论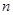 的范围,确定
的范围,确定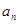 与
与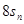 的大小.此题考察了等差数列的基本知识,运算量比较大,属于中档题,
的大小.此题考察了等差数列的基本知识,运算量比较大,属于中档题,试题解析:(1)因
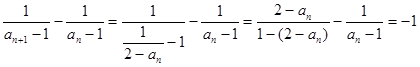 , 3分
, 3分故数列
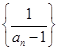 是首项为-4,公差为-1的等差数列, 5分
是首项为-4,公差为-1的等差数列, 5分所以
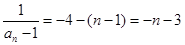 ,即
,即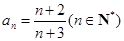 . 7分
. 7分(2)因
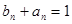 ,故
,故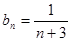 ,则
,则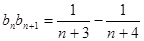 , 9分
, 9分于是
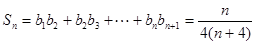 , 11分
, 11分从而
 , 12分
, 12分所以,当
 时,
时,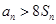 ;当
;当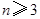 时,
时, . 14分
. 14分
练习册系列答案
 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案
相关题目
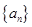 满足
满足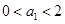 ,
,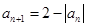 ,
,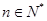 .
.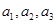 成等比数列,求
成等比数列,求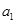 的值;
的值;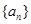 的前3项和
的前3项和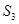 =9,且
=9,且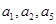 成等比数列
成等比数列 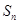 ;
;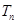 为数列
为数列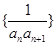 的前n项和,若
的前n项和,若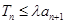 对一切
对一切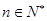 恒成立,求实数
恒成立,求实数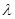 的最小值
的最小值 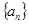 ,
,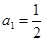 ,且满足
,且满足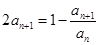 .
.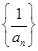 是等差数列;
是等差数列;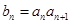 ,求数列
,求数列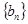 的前n项和
的前n项和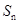 .
.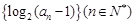 为等差数列,且
为等差数列,且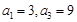 .
.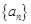 的通项公式;
的通项公式;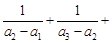 …
…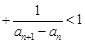 .
.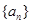 中,已知
中,已知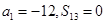 ,使得
,使得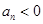 的最大正整数
的最大正整数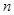 为( )
为( )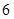
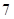
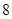
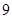
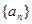 的前n项和为Sn,
的前n项和为Sn,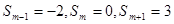 ,则正整数m的值为_____________.
,则正整数m的值为_____________.