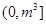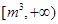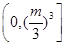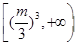题目内容
设等比数列{an}的前n项和为Sn,a4=a1-9,a5,a3,a4成等差数列.
(1)求数列{an} 的通项公式;
(2)证明:对任意k∈N*,Sk+2,Sk,Sk+1成等差数列.
(1)求数列{an} 的通项公式;
(2)证明:对任意k∈N*,Sk+2,Sk,Sk+1成等差数列.
(1)an=(-2)n-1n∈N*(2)见解析
(1)解:在等比数列{an}中,a5,a3,a4成等差数列,
∴2a3=a5+a4,
即2a1q2=a1q4+a1q3,整理得:q2+q-2=0.
解得q=1,或q=-2.
又a4=a1-9,即a1q3=a1-9,
当q=1时,无解.
当q=-2时,解得a1=1
∴等比数列{an}通项公式为an=(-2)n-1n∈N*
(2)证明:∵Sn为等比数列{an}的前n项和,
∴Sk=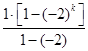 =
=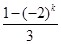 ,Sk+1=
,Sk+1=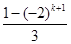 ,Sk+2=
,Sk+2=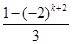 ,
,
∵Sk+1+Sk+2=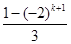 +
+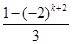 =
=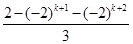 =
=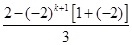 =
=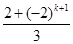 =2·
=2·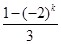 =2Sk.
=2Sk.
∴Sk+1,Sk,Sk+2成等差数列.
∴2a3=a5+a4,
即2a1q2=a1q4+a1q3,整理得:q2+q-2=0.
解得q=1,或q=-2.
又a4=a1-9,即a1q3=a1-9,
当q=1时,无解.
当q=-2时,解得a1=1
∴等比数列{an}通项公式为an=(-2)n-1n∈N*
(2)证明:∵Sn为等比数列{an}的前n项和,
∴Sk=
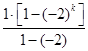 =
=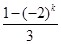 ,Sk+1=
,Sk+1=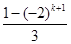 ,Sk+2=
,Sk+2=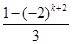 ,
,∵Sk+1+Sk+2=
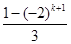 +
+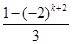 =
=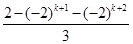 =
=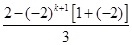 =
=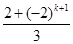 =2·
=2·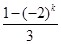 =2Sk.
=2Sk.∴Sk+1,Sk,Sk+2成等差数列.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
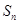 表示数列
表示数列 的前
的前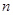 项和.
项和. 的等比数列,写出并推导
的等比数列,写出并推导 ,
,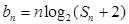 ,求证:
,求证: <1.
<1.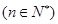 个正数
个正数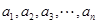 使得这
使得这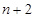 个数构成递增的等比数列,将这
个数构成递增的等比数列,将这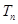 ,令
,令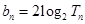 .
.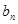 }的通项公式;
}的通项公式;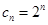 ,设
,设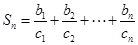 ,求
,求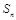 .
.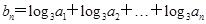 ,求数列
,求数列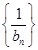 的前n项和.
的前n项和.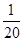 ,9S3=S6,设Tn=a1a2a3…an,则使Tn取最小值的n值为( ).
,9S3=S6,设Tn=a1a2a3…an,则使Tn取最小值的n值为( ).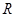 上的函数
上的函数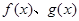 满足
满足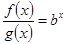 ,且
,且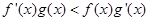 ,
, 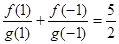 ,若
,若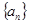 是正项等比数列,且
是正项等比数列,且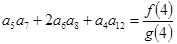 ,则
,则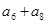 等于 .
等于 .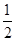 ,a4=-4,则|a1|+|a2|+…+|an|=________.
,a4=-4,则|a1|+|a2|+…+|an|=________.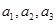 的和为定值
的和为定值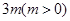 ,且公比为
,且公比为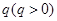 ,令
,令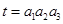 ,则
,则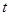 的取值范围为( )
的取值范围为( )