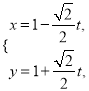[题目]已知圆的半径为,圆心在直线y=2x上,圆被直线x-y=0截得的弦长为4,求圆的方程. 题目和参考答案——青夏教育精英家教网—

题目内容

【题目】已知圆的半径为,圆心在直线y=2x上,圆被直线x-y=0截得的弦长为4,求圆的方程.

【答案】或

【解析】试题分析：设圆的方程是，根据圆心在直线上,所以 .①联立方程组，，由弦长公式得 ,化简得 .②

解①②组成的方程组,求出，即可求出圆的方程．

试题解析：设圆的方程是(x-a)2+(y-b)2=10，因为圆心在直线y=2x上,所以b=2a.①

解方程组得2x2-2(a+b)x+a2+b2-10=0,

所以x1+x2=a+b,x1·x2=，由弦长公式得·=4,化简得(a-b)2=4.②

解①②组成的方程组,得a=2,b=4,或a=-2,b=-4，

故所求圆的方程是(x-2)2+(y-4)2=10,或(x+2)2+(y+4)2=10.

练习册系列答案

t(年)	1	2	3	4	5	6
h(米)	0.6	1	1.3	1.5	1.6	1.7

【题目】如图是一建筑物的三视图(单位： )，现需将其外壁用油漆粉刷一遍，已知每平方米用漆，问需要油漆多少千克？(无需求近似值)

【题目】定义在上的函数，如果满足：对任意，存在常数，都有成立，则称是上的有界函数，其中称为函数的上界，已知函数.

（1）当时，求函数在上的值域，并判断函数在上是否为有界函数，请说明理由；

（2）若函数在上是以4为上界的有界函数，求实数的取值范围.

【题目】选修4-4：坐标系与参数方程

在平面直角坐标系中，直线的参数方程为为参数).它与曲线交于两点.

（1）求的长；

（2）在以为极点，轴的正半轴为极轴建立极坐标系，设点的极坐标为，求点到线段中点的距离.

【题目】近年来，“共享单车”的出现为市民“绿色出行”提供了极大的方便，某共享单车公司“Mobike”计划在甲、乙两座城市共投资120万元，根据行业规定，每个城市至少要投资40万元，由前期市场调研可知：甲城市收益与投入（单位：万元）满足，乙城市收益与投入（单位：万元）满足，设甲城市的投入为（单位：万元），两个城市的总收益为（单位：万元）。