题目内容
14.已知抛物线C:y2=4x,过定点(2,0)作垂直于x轴的直线交抛物线于点M、N,若P为抛物线C上不同于M、N的任意一点,若直线PM、PN的斜率都存在并记为k1、k2,则|$\frac{1}{k_1}-\frac{1}{k_2}$|=( )| A. | 2 | B. | 1 | C. | $\sqrt{2}$ | D. | $2\sqrt{2}$ |
分析 取特殊点P(0,0),$M(2,2\sqrt{2}),N(2,-2\sqrt{2})$,求出k1、k2,即可求出|$\frac{1}{k_1}-\frac{1}{k_2}$|.
解答 解:取特殊点P(0,0),$M(2,2\sqrt{2}),N(2,-2\sqrt{2})$,则${k_1}=\sqrt{2},{k_2}=-\sqrt{2}$,
所以$|\frac{1}{k_1}-\frac{1}{k_2}|=\sqrt{2}$.
故选:C.
点评 本题考查直线与抛物线的位置关系,考查特殊法的运用,比较基础.

练习册系列答案
相关题目
4.在△ABC中,A=60°,若a,b,c成等比数列,则$\frac{bsinB}{c}$=( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{6}+\sqrt{2}}{4}$ |
9.下列判断中正确的是( )
| A. | 命题“若a-b=1,则a2+b2>$\frac{1}{2}$”是真命题 | |
| B. | “a=b=$\frac{1}{2}$”是“$\frac{1}{a}+\frac{1}{b}$=4”的必要不充分条件 | |
| C. | 若非空集合A,B,C满足A∪B=C,且B不是A的子集,则“x∈C”是“x∈A”的充分不必要条件 | |
| D. | 命题“?x0∈R,x02+1≤2x0”的否定是“?x∈R,x2+1>2x” |
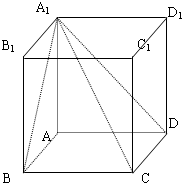 如图,长方体ABCD-A1B1C1D1的AA1=1,底面ABCD的周长为4.
如图,长方体ABCD-A1B1C1D1的AA1=1,底面ABCD的周长为4.