题目内容
4.△ABC中,周长为6,a,b,c三边成等比数列,求三角形面积最大值.分析 由a、b、c成等比数列得b2=ac,由余弦定理和基本不等式,即可得到B的范围,由周长为6和基本不等式求出b的范围,代入三角形的面积公式可求出面积的最大值.
解答 解:∵a、b、c成等比数列,∴b2=ac,
由余弦定理得:cosB=$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$=$\frac{{a}^{2}+{c}^{2}-ac}{2ac}$≥$\frac{2ac-ac}{2ac}$=$\frac{1}{2}$,
当且仅当a=c时取等号,
∵0<B<π,∴0<B≤$\frac{π}{3}$,
∵三角形周长为6,b2=ac,∴a+b+c=6,
∵a+c≥2$\sqrt{ac}$=2b(当且仅当a=c时取等号),∴6-b≥2b,即0<b≤2,
则b的取值范围是(0,2];
∴△ABC的面积S=$\frac{1}{2}$acsinB=$\frac{1}{2}$b2sinB≤$\frac{1}{2}×4×sin\frac{π}{3}$=$\sqrt{3}$,
∴当且仅当a=c=b=2、B=$\frac{π}{3}$时,三角形面积取最大值是$\sqrt{3}$.
点评 本题考查了余弦定理,三角形的面积公式的应用,以及基本不等式求最值的应用,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.已知抛物线C:y2=4x,过定点(2,0)作垂直于x轴的直线交抛物线于点M、N,若P为抛物线C上不同于M、N的任意一点,若直线PM、PN的斜率都存在并记为k1、k2,则|$\frac{1}{k_1}-\frac{1}{k_2}$|=( )
| A. | 2 | B. | 1 | C. | $\sqrt{2}$ | D. | $2\sqrt{2}$ |
12.如表是对与喜欢足球与否的统计列联表依据表中的数据,得到( )
| 喜欢足球 | 不喜欢足球 | 总计 | |
| 男 | 40 | 28 | 68 |
| 女 | 5 | 12 | 17 |
| 总计 | 45 | 40 | 85 |
| A. | K2=9.564 | B. | K2=3.564 | C. | K2<2.706 | D. | K2>3.841 |
19.设随机变量X:B(6,$\frac{1}{3}$),则D(X)等于( )
| A. | 2 | B. | $\frac{4}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{8}{3}$ |
16.已知函数f(x)=$\left\{\begin{array}{l}|x+1|,-7≤x≤0\\ 1nx,{e^{-2}}≤x≤e\end{array}$,g(x)=x2-2x,设a为实数,若存在实数m,使f(m)-2g(a)=0,则实数a的取值范围为( )
| A. | [-1,+∞) | B. | (-∞,-1]∪[3,+∞) | C. | [-1,3] | D. | (-∞,3] |
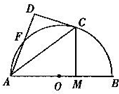 如图,AB是圆O的直径,C、F为圆O上点,CA是∠BAF的角平分线,CD与圆O切于点C且交AF的延长线于点D,CM⊥AB,垂足为点M,求证:
如图,AB是圆O的直径,C、F为圆O上点,CA是∠BAF的角平分线,CD与圆O切于点C且交AF的延长线于点D,CM⊥AB,垂足为点M,求证: