题目内容
16．已知x，y满足约束条件$\left\{\begin{array}{l}{x≤1}\\{x-y+1≥0}\\{-2x-y+2≤0}\end{array}\right.$，则$\sqrt{{x}^{2}+{y}^{2}}$的最小值为（ ）| A． | $\sqrt{5}$ | B． | $\frac{2\sqrt{5}}{5}$ | C． | 1 | D． | $\frac{\sqrt{5}}{2}$ |
分析 作出不等式组对应的平面区域，利用z的几何意义进行求解即可．
解答 解：作出约束条件$\left\{\begin{array}{l}{x≤1}\\{x-y+1≥0}\\{-2x-y+2≤0}\end{array}\right.$对应的平面区域如图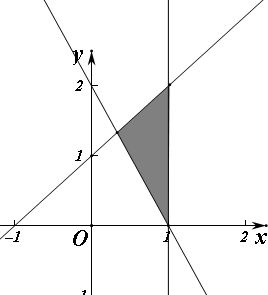
，
z的几何意义为区域内的点到原点的距离的平方，
由图象知：原点O到直线-2x-y+2=0的距离为所求，原点到直线的距离为$\frac{|2|}{\sqrt{（-2）^{2}+（-1）^{2}}}=\frac{2}{\sqrt{5}}=\frac{2\sqrt{5}}{5}$，故所求为$\frac{2\sqrt{5}}{5}$；
故选B．
点评 本题主要考查线性规划的应用以及点到直线的距离公式的应用，利用数形结合是解决本题的关键．
练习册系列答案
一本好题口算题卡系列答案
相关题目
4．已知集合M={t|t=a+$\sqrt{2}$b，a，b∈Z}，设x，y∈M，则（ ）
| A． | x±y∉M | B． | xy∈M，x+y∉M | C． | xy∉m | D． | x±y∈M，xy∈M |
11．对某元件进行寿命追踪调查情况如下：
列出频率分布表．
| 寿命/h | 250～300 | 300～350 | 350～400 | 400～450 | 450～500 |
| 个数 | 40 | 60 | 160 | 80 | 60 |
1．函数y=2cosx+1的对称轴是（ ）
| A． | x=kπ，（k∈Z） | B． | x=kπ+$\frac{π}{2}$，（k∈Z） | C． | x=2kπ+$\frac{π}{2}$，（k∈Z） | D． | x=2kπ-$\frac{π}{2}$，（k∈Z） |