题目内容
6.函数y=$\frac{2x+1}{x+a}$在(-2,+∞)上单调递增,则实数a的取值范围[2,+∞).分析 化简函数,利用函数y=$\frac{2x+1}{x+a}$在(-2,+∞)上单调递增,可得1-2a<0且-a≤-2,从而求得a的取值范围.
解答 解:y=$\frac{2x+1}{x+a}$=2+$\frac{1-2a}{x+a}$.
∵函数y=$\frac{2x+1}{x+a}$在(-2,+∞)上单调递增,
∴1-2a<0且-a≤-2,∴a≥2;
∴a的取值范围是:[2,+∞).
故答案为:[2,+∞).
点评 本题考查函数单调性,考查学生的计算能力,正确化简函数是求解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.已知x,y满足约束条件$\left\{\begin{array}{l}{x≤1}\\{x-y+1≥0}\\{-2x-y+2≤0}\end{array}\right.$,则$\sqrt{{x}^{2}+{y}^{2}}$的最小值为( )
| A. | $\sqrt{5}$ | B. | $\frac{2\sqrt{5}}{5}$ | C. | 1 | D. | $\frac{\sqrt{5}}{2}$ |
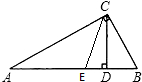 如图,Rt△ABC被斜边上的高CD和直角平分线CE分成3个三角形,S△ACE=30,S△CED=6,则△BCD的面积为( )
如图,Rt△ABC被斜边上的高CD和直角平分线CE分成3个三角形,S△ACE=30,S△CED=6,则△BCD的面积为( )