题目内容
3.已知点A(1,3),B(3,1),点C是直线l1:3x-2y+3=0和直线l2:2x-y+2=0的交点.(1)求l1与l2的交点C的坐标;
(2)求△ABC的面积.
分析 (1)联立直线方程,解方程组可得;
(2)由距离公式可得|AB|和AB上的高h,代入三角形的面积公式可得.
解答 解:(1)联立方程组$\left\{\begin{array}{l}3x-2y+3=0\\ 2x-y+2=0\end{array}\right.$,解得$\left\{\begin{array}{l}x=-1\\ y=0.\end{array}\right.$
∴l1与l2的交点C的坐标为(-1,0);
(2)设AB上的高为h,则${S_{△ABC}}=\frac{1}{2}|{AB}|•h$,
由距离公式可得$|AB|=\sqrt{{{(3-1)}^2}+{{(1-3)}^2}}=2\sqrt{2}$,
AB边上的高h就是点C到AB的距离.
AB边所在直线方程为$\frac{y-3}{1-3}=\frac{x-1}{3-1}$,即x+y-4=0,
点C到x+y-4=0的距离为$h=\frac{|-1+0-4|}{{\sqrt{{1^2}+{1^2}}}}=\frac{5}{{\sqrt{2}}}$,
∴${S_{△ABC}}=\frac{1}{2}×2\sqrt{2}×\frac{5}{{\sqrt{2}}}=5$
点评 本题考查直线的交点坐标和距离公式,涉及三角形的面积,属基础题.

练习册系列答案
相关题目
13.设Sn为正项等比数列{an}的前n项和,且4a1-a3=0,则$\frac{{S}_{3}}{{a}_{1}}$=( )
| A. | 3 | B. | 7 | C. | $\frac{7}{4}$ | D. | 3或7 |
14.已知命题p:若x>y,则-x<-y;命题q:若x<y,则x2>y2;在下列命题中:(1)p∧q;(2)p∨q;(3)p∧(¬q);(4)(¬p)∨q,真命题是( )
| A. | (1)(3) | B. | (1)(4) | C. | (2)(3) | D. | (2)(4) |
11.若某空间几何体的三视图如图所示,则该几何体的体积为( )
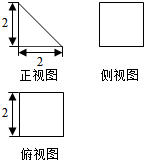

| A. | $\frac{8}{3}$ | B. | 8 | C. | 4 | D. | $\frac{4}{3}$ |
15.已知直角三角形的两直角边长的和为4,则此直角三角形的面积满足( )
| A. | 最大值2 | B. | 最大值4 | C. | 最小值2 | D. | 最小值4 |
12.已知向量$\overrightarrow{a}$=(4,2),$\overrightarrow{b}$=(x,3),若$\overrightarrow{a}$∥$\overrightarrow{b}$,则实数x的值为( )
| A. | 3 | B. | 6 | C. | $\frac{3}{2}$ | D. | $\frac{2}{3}$ |
 设抛物线C:y2=x与直线l交于A,B两点(异于原点O),以AB为直径的圆恰好经过原点O.
设抛物线C:y2=x与直线l交于A,B两点(异于原点O),以AB为直径的圆恰好经过原点O.