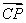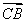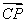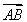题目内容
如图,在边长为4的菱形ABCD中,∠DAB=60°,点E、F分别在边CD、CB上,点E与点C、D不重合,EF⊥AC,EF∩AC=O,沿EF将△CEF翻折到△PEF的位置,使平面PEF⊥平面ABFED.
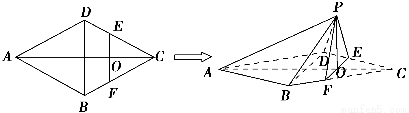
(1)求证:BD⊥平面POA;
(2)记三棱锥P ?ABD体积为V1,四棱锥P ?BDEF体积为V2,且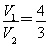 ,求此时线段PO的长.
,求此时线段PO的长.
(1)见解析(2)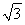
【解析】(1)在菱形ABCD中,∵BD⊥AC,
∴BD⊥AO.
∵EF⊥AC,∴PO⊥EF,
∵平面PEF⊥平面ABFED,平面PEF∩平面ABFED=EF,且PO?平面PEF.
∴PO⊥平面ABFED,
∵BD?平面ABFED,
∴PO⊥BD.
∵AO∩PO=O,AO,PO?平面POA.
∴BD⊥平面POA.
(2)设AO∩BD=H
由(1)知,PO⊥平面ABFED,PO=CO.
∴PO是三棱锥P?ABD的高及四棱锥P?BDEF的高
∴V1= S△ABD·PO,V2=
S△ABD·PO,V2=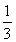 S梯形BFED·PO
S梯形BFED·PO
∵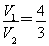 ∴S梯形BFED=
∴S梯形BFED= S△ABD=
S△ABD=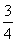 S△BCD
S△BCD
∴S△CEF=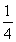 S△BCD
S△BCD
∵BD⊥AC,EF⊥AC,∴EF∥BD,∴△CEF∽△CDB
∴ =
=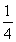
∴CO=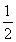 CH=
CH=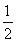 AH=
AH=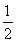 ×2
×2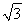 =
=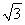
∴线段PO的长为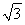 .
.

练习册系列答案
相关题目