题目内容
若函数f(x)=a-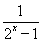 是定义在(-∞,-1]∪[1,+∞)上的奇函数,则f(x)的值域为________.
是定义在(-∞,-1]∪[1,+∞)上的奇函数,则f(x)的值域为________.
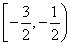 ∪
∪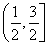
【解析】由题意可得f(-1)=-f(1),解得a=- ,所以f(x)=-
,所以f(x)=- -
-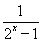 ,当x≥1时,得f(x)为增函数,2x≥2,2x-1≥1,∴0<
,当x≥1时,得f(x)为增函数,2x≥2,2x-1≥1,∴0<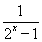 ≤1,∴-
≤1,∴-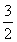 ≤f(x)<-
≤f(x)<- .由对称性知,当x≤-1时,
.由对称性知,当x≤-1时,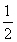 <f(x)≤
<f(x)≤ .
.
综上,所求值域为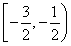 ∪
∪ .
.

练习册系列答案
相关题目
题目内容
若函数f(x)=a-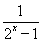 是定义在(-∞,-1]∪[1,+∞)上的奇函数,则f(x)的值域为________.
是定义在(-∞,-1]∪[1,+∞)上的奇函数,则f(x)的值域为________.
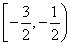 ∪
∪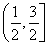
【解析】由题意可得f(-1)=-f(1),解得a=- ,所以f(x)=-
,所以f(x)=- -
-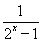 ,当x≥1时,得f(x)为增函数,2x≥2,2x-1≥1,∴0<
,当x≥1时,得f(x)为增函数,2x≥2,2x-1≥1,∴0<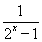 ≤1,∴-
≤1,∴-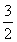 ≤f(x)<-
≤f(x)<- .由对称性知,当x≤-1时,
.由对称性知,当x≤-1时,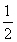 <f(x)≤
<f(x)≤ .
.
综上,所求值域为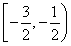 ∪
∪ .
.
