题目内容
已知函数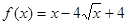 (x≥4)的反函数为
(x≥4)的反函数为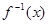 ,数列
,数列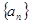 满足:a1=1,
满足:a1=1,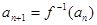 ,(
,(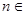 N*),数列
N*),数列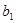 ,
,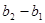 ,
,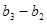 ,…,
,…,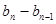 是首项为1,公比为
是首项为1,公比为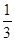 的等比数列.
的等比数列.
(Ⅰ)求证:数列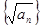 为等差数列; (Ⅱ)若
为等差数列; (Ⅱ)若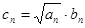 ,求数列
,求数列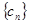 的前n项和
的前n项和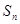 .
.
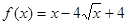 (x≥4)的反函数为
(x≥4)的反函数为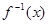 ,数列
,数列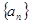 满足:a1=1,
满足:a1=1,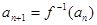 ,(
,(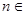 N*),数列
N*),数列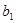 ,
,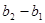 ,
,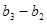 ,…,
,…,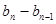 是首项为1,公比为
是首项为1,公比为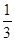 的等比数列.
的等比数列.(Ⅰ)求证:数列
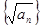 为等差数列; (Ⅱ)若
为等差数列; (Ⅱ)若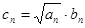 ,求数列
,求数列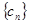 的前n项和
的前n项和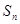 .
.(Ⅰ)见解析; (Ⅱ)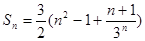 .
.
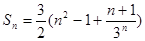 .
.(I)反解x,可得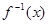
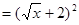 (x≥0),
(x≥0),
所以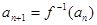
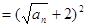 ,从而可得
,从而可得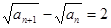 (
(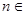 N*),由等差数列的定义可知数列
N*),由等差数列的定义可知数列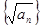 是等差数列.
是等差数列.
(II)由题意可知当n≥2时,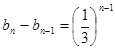 ,然后采用叠加的办法求出
,然后采用叠加的办法求出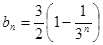 ,从而确定
,从而确定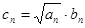
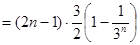 ,然后采用错位相减的方法求和.
,然后采用错位相减的方法求和.
(Ⅰ)∵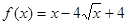
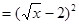 (x≥4),
(x≥4),
∴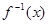
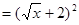 (x≥0),
(x≥0),
∴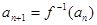
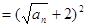 ,
,
即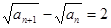 (
(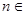 N*).
N*).
∴数列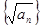 是以
是以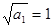 为首项,公差为2的等差数列.
为首项,公差为2的等差数列.
(Ⅱ)由(Ⅰ)得: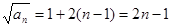 ,即
,即
 (
(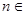 N*).
N*).
b1=1,当n≥2时,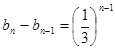 ,
,
∴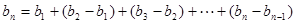
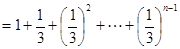
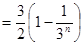
因而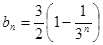 ,
,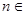 N*.
N*.
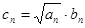
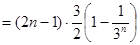 ,
,
∴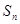

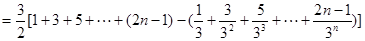
令
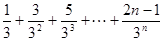 ①
①
则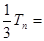
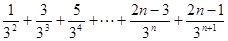 ②
②
①-②,得
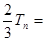
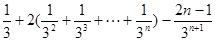
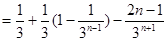
∴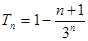 .又
.又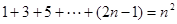 .
.
∴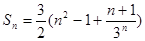 .
.
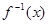
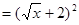 (x≥0),
(x≥0),所以
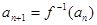
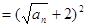 ,从而可得
,从而可得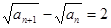 (
(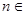 N*),由等差数列的定义可知数列
N*),由等差数列的定义可知数列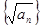 是等差数列.
是等差数列.(II)由题意可知当n≥2时,
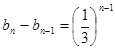 ,然后采用叠加的办法求出
,然后采用叠加的办法求出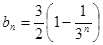 ,从而确定
,从而确定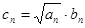
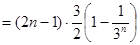 ,然后采用错位相减的方法求和.
,然后采用错位相减的方法求和.(Ⅰ)∵
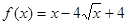
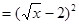 (x≥4),
(x≥4),∴
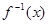
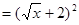 (x≥0),
(x≥0), ∴
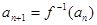
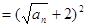 ,
,即
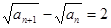 (
(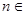 N*).
N*).∴数列
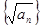 是以
是以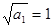 为首项,公差为2的等差数列.
为首项,公差为2的等差数列. (Ⅱ)由(Ⅰ)得:
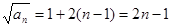 ,即
,即 (
(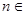 N*).
N*).b1=1,当n≥2时,
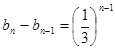 ,
,∴
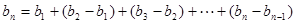
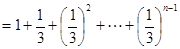
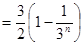
因而
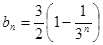 ,
,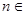 N*.
N*. 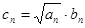
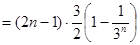 ,
,∴
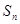

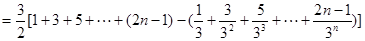
令

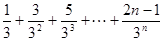 ①
①则
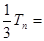
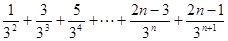 ②
②①-②,得
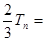
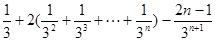
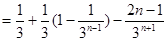
∴
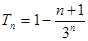 .又
.又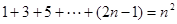 .
.∴
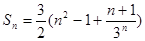 .
.
练习册系列答案
相关题目
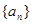 的首项为
的首项为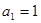 ,前n项和
,前n项和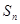 满足关系式:
满足关系式: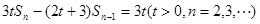
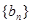 ,使得
,使得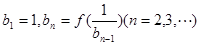 ,求:b
,求:b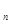 及
及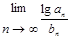 ;
;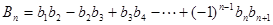 。
。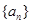 是公比大于1的等比数列,
是公比大于1的等比数列,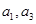 是函数
是函数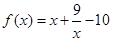 的两个零点。
的两个零点。 满足
满足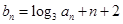 ,且
,且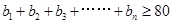 ,求
,求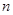 的最小值。
的最小值。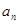 }的前n项和为
}的前n项和为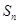 ,若
,若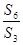 =3,则
=3,则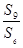 =
=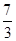
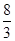
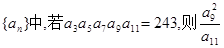 的值为( )
的值为( ) 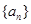 的前
的前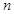 项和为
项和为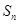 ,
,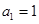 , 若
, 若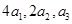 成等差数列,则
成等差数列,则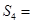 ( )
( ) 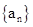 中,
中,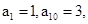 则
则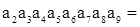 ( )
( )