题目内容
已知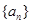 是公比大于1的等比数列,
是公比大于1的等比数列,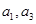 是函数
是函数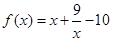 的两个零点。
的两个零点。
(1)求数列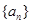 的通项公式;
的通项公式;
(2)若数列 满足
满足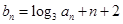 ,且
,且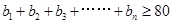 ,求
,求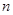 的最小值。
的最小值。
 是公比大于1的等比数列,
是公比大于1的等比数列,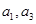 是函数
是函数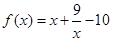 的两个零点。
的两个零点。(1)求数列
 的通项公式;
的通项公式;(2)若数列
 满足
满足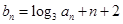 ,且
,且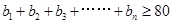 ,求
,求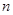 的最小值。
的最小值。
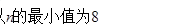
本题考查数列{an}的通项公式的求法和求n的最小值.解题时要认真审题,注意等比数列的通项公式和等差数列前n项和公式的灵活运用.
(1)由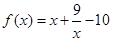 ,得x2-10x+9=0,解得x1=1,x2=9,由{an}是公比q大于1的等比数列,a1,a3是函数
,得x2-10x+9=0,解得x1=1,x2=9,由{an}是公比q大于1的等比数列,a1,a3是函数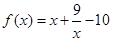 的的两个零点,知a1=1,a3=9,由此能求出数列{an}的通项公式.
的的两个零点,知a1=1,a3=9,由此能求出数列{an}的通项公式.
(2)由an=3n-1,知bn=log3an+n+2=log33n-1+n+2=2n+1,由此得到b1+b2+b3+…+bn=n2+2n,由b1+b2+b3+…+bn≥80,得n2+2n≥80,由此能求出n的最小值
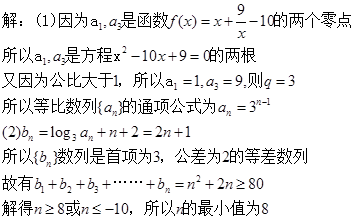
(1)由
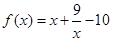 ,得x2-10x+9=0,解得x1=1,x2=9,由{an}是公比q大于1的等比数列,a1,a3是函数
,得x2-10x+9=0,解得x1=1,x2=9,由{an}是公比q大于1的等比数列,a1,a3是函数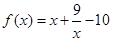 的的两个零点,知a1=1,a3=9,由此能求出数列{an}的通项公式.
的的两个零点,知a1=1,a3=9,由此能求出数列{an}的通项公式.(2)由an=3n-1,知bn=log3an+n+2=log33n-1+n+2=2n+1,由此得到b1+b2+b3+…+bn=n2+2n,由b1+b2+b3+…+bn≥80,得n2+2n≥80,由此能求出n的最小值
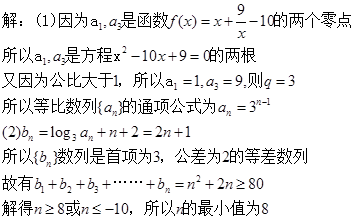

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
 的公差
的公差 ,设
,设 ,
,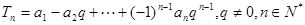
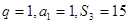 ,求数列
,求数列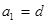 ,且
,且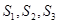 成等比数列,求
成等比数列,求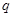 的值;
的值;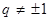 ,证明:
,证明: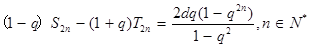 .
.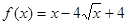 (x≥4)的反函数为
(x≥4)的反函数为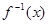 ,数列
,数列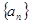 满足:a1=1,
满足:a1=1,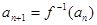 ,(
,(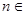 N*),数列
N*),数列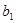 ,
,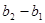 ,
,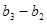 ,…,
,…,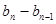 是首项为1,公比为
是首项为1,公比为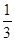 的等比数列.
的等比数列.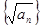 为等差数列; (Ⅱ)若
为等差数列; (Ⅱ)若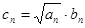 ,求数列
,求数列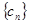 的前n项和
的前n项和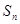 .
.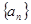 ,公比
,公比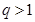 ,且
,且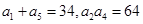 ,
, 满足
满足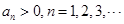 且
且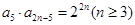 ,则
,则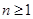 时,
时,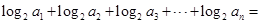 ( )
( )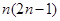
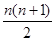
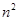
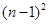
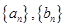 满足
满足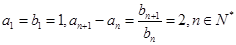 ,则数列
,则数列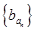 的前10项和为( )
的前10项和为( )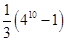

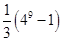
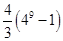
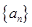 中,
中,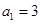 ,前三项和为21,则
,前三项和为21,则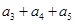 等于( )
等于( ) 中,
中,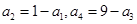 ,则
,则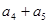 等于( )
等于( )