题目内容
定义: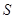 为
为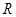 的真子集,
的真子集,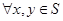 ,若
,若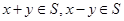 ,则称
,则称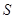 对加减法封闭。有以下四个命题,请判断真假:
对加减法封闭。有以下四个命题,请判断真假:
①自然数集对加减法封闭;
②有理数集对加减法封闭;
③若有理数集对加减法封闭,则无理数集也对加减法封闭;
④若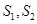 为
为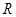 的两个真子集,且对加减法封闭,则必存在
的两个真子集,且对加减法封闭,则必存在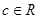 ,使得
,使得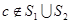 ;
;
四个命题中为“真”的是 ;(填写序号)
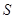 为
为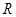 的真子集,
的真子集,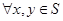 ,若
,若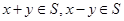 ,则称
,则称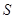 对加减法封闭。有以下四个命题,请判断真假:
对加减法封闭。有以下四个命题,请判断真假:①自然数集对加减法封闭;
②有理数集对加减法封闭;
③若有理数集对加减法封闭,则无理数集也对加减法封闭;
④若
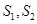 为
为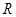 的两个真子集,且对加减法封闭,则必存在
的两个真子集,且对加减法封闭,则必存在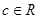 ,使得
,使得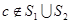 ;
;四个命题中为“真”的是 ;(填写序号)
②④;
当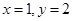 时,
时, ,但
,但 ,所以命题①不正确;
,所以命题①不正确;
任意两个有理数的和和差都还是有理数,所以命题②正确;
当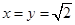 时,
时,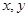 都是无理数,但
都是无理数,但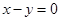 是有理数,所以命题③不正确;
是有理数,所以命题③不正确;
令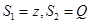 ,则
,则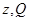 是
是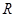 的两个真子集,且对加减法封闭。则存在
的两个真子集,且对加减法封闭。则存在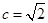 ,使得
,使得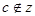 且
且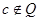 ,所以
,所以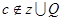 ,所以命题④正确。
,所以命题④正确。
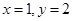 时,
时, ,但
,但 ,所以命题①不正确;
,所以命题①不正确;任意两个有理数的和和差都还是有理数,所以命题②正确;
当
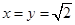 时,
时,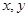 都是无理数,但
都是无理数,但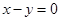 是有理数,所以命题③不正确;
是有理数,所以命题③不正确;令
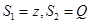 ,则
,则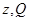 是
是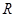 的两个真子集,且对加减法封闭。则存在
的两个真子集,且对加减法封闭。则存在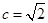 ,使得
,使得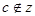 且
且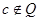 ,所以
,所以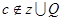 ,所以命题④正确。
,所以命题④正确。
练习册系列答案
相关题目
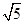 i,z2=
i,z2=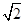 -
-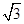 i,z3=-
i,z3=-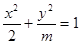 表示焦点在y轴上的椭圆”,
表示焦点在y轴上的椭圆”,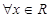 ,
,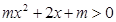 恒成立”,
恒成立”,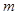 的取值范围。
的取值范围。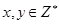 ,若
,若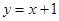 ,则
,则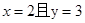 .
.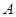 、
、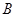 为两个定点,
为两个定点,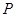 为动点,且
为动点,且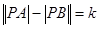 ,其中常数
,其中常数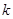 为正实数,则动点
为正实数,则动点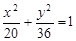 ;
;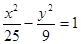 与椭圆
与椭圆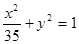 有相同的焦点.
有相同的焦点.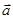 ,
, 的夹角为锐角”的充要条件是“
的夹角为锐角”的充要条件是“ )>
)>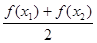 ;
;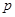 且
且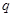 是真命题”, 命题乙:“
是真命题”, 命题乙:“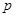 :存在
:存在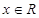 ,使
,使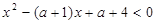 ;命题
;命题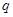 :方程
:方程 表示双曲线.若命题“
表示双曲线.若命题“ ”为真命题,求实数
”为真命题,求实数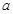 的取值范围.
的取值范围.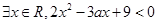 ”为假命题,则实数a的取值区间为
”为假命题,则实数a的取值区间为