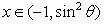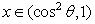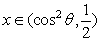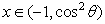题目内容
设函数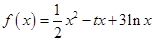 ,
, ,已知
,已知 为函数
为函数 的极值点
的极值点
(1)求函数 在
在 上的单调区间,并说明理由.
上的单调区间,并说明理由.
(2)若曲线 在
在 处的切线斜率为-4,且方程
处的切线斜率为-4,且方程 有两个不相等的负实根,求实数
有两个不相等的负实根,求实数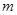 的取值范围.
的取值范围.
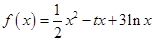 ,
, ,已知
,已知 为函数
为函数 的极值点
的极值点
(1)求函数
 在
在 上的单调区间,并说明理由.
上的单调区间,并说明理由.(2)若曲线
 在
在 处的切线斜率为-4,且方程
处的切线斜率为-4,且方程 有两个不相等的负实根,求实数
有两个不相等的负实根,求实数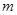 的取值范围.
的取值范围.(1)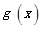 的单调增区间为
的单调增区间为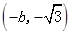 和
和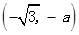 ,
,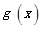 的单调减区间为
的单调减区间为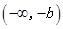
(2)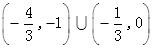 .
.
 的单调增区间为
的单调增区间为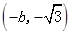 和
和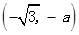 ,
,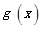 的单调减区间为
的单调减区间为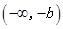
(2)
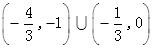 .
.试题分析:(1)
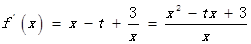 ,
,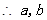 为方程
为方程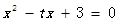 的两根
的两根又
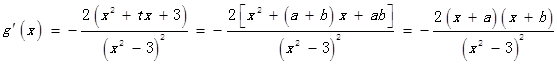
由
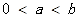 及
及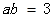 知:
知:
当
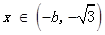 和
和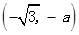 时,
时,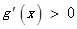 ,当
,当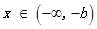 时,
时,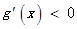
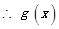 的单调增区间为
的单调增区间为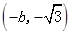 和
和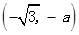 ,
, 的单调减区间为
的单调减区间为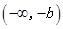
(2)由
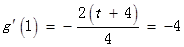 得
得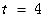
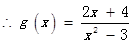
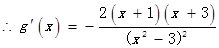
令
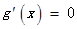 得
得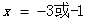
当
 在
在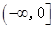 上变化时,
上变化时,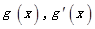 的变化情况如下:
的变化情况如下: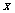 | 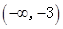 | -3 | 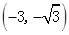 | 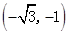 | 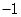 - - | 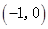 | 0 |
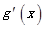 | - | 0 | + | + | 0 | - | |
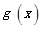 | ↘ | 极小值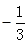 | ↗ | ↗ | 极大值 | ↘ | 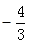 |
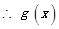 的大致图象如图
的大致图象如图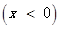

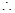 方程
方程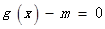 有两个不等的负实根时,
有两个不等的负实根时,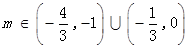 .
.点评:近几年新课标高考对于函数与导数这一综合问题的命制,一般以有理函数与半超越(指数、对数)函数的组合复合且含有参量的函数为背景载体,解题时要注意对数式对函数定义域的隐蔽,这类问题重点考查函数单调性、导数运算、不等式方程的求解等基本知识,注重数学思想(分类与整合、数与形的结合)方法(分析法、综合法、反证法)的运用.把数学运算的“力量”与数学思维的“技巧”完美结合

练习册系列答案
相关题目
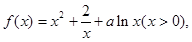
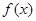 在
在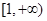 上单调递增,求
上单调递增,求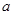 的取值范围;
的取值范围;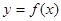 对于区间
对于区间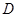 上的任意两个值
上的任意两个值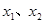 总有以下不等式
总有以下不等式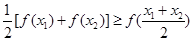 成立,则称函数
成立,则称函数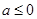 时,
时, 上的减函数的是( )
上的减函数的是( )


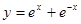
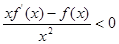 成立,则不等式
成立,则不等式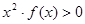 的解集是( )
的解集是( )
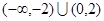
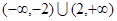

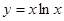 的单调递减区间是( )
的单调递减区间是( )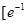 ,+∞)
,+∞)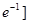
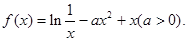
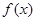 是定义域上的单调函数,求
是定义域上的单调函数,求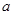 的取值范围;
的取值范围;
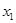 、
、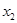 ,证明:
,证明: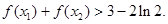
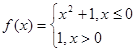 ,则满足不等式
,则满足不等式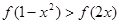 的实数x的取值范围是__________________。
的实数x的取值范围是__________________。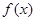 满足
满足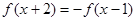 ,则6为函数
,则6为函数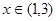 ,不等式
,不等式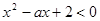 恒成立,则
恒成立,则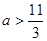 ;
;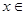 R,都存在正常数
R,都存在正常数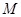 ,使
,使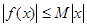 恒成立,则称函数
恒成立,则称函数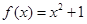 为有界泛函;
为有界泛函;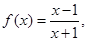 设
设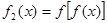 ,
,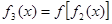 ,…,
,…,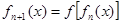 (
(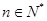 且
且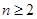 ),令集合
),令集合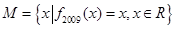 ,则集合
,则集合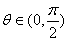 ,则函数
,则函数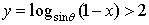 的解集是( )
的解集是( )