题目内容
已知函数f(x)是定义在R上的奇函数,f(2)=0,当x>0时,有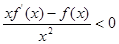 成立,则不等式
成立,则不等式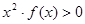 的解集是( )
的解集是( )
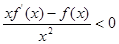 成立,则不等式
成立,则不等式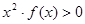 的解集是( )
的解集是( )A. | B.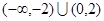 |
C.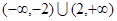 | D. |
B
试题分析:解:因为当x>0时,有
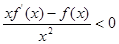 恒成立,即[
恒成立,即[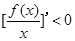
恒成立,所以
 在(0,+∞)内单调递减.因为f(2)=0,所以在(0,2)内恒有
在(0,+∞)内单调递减.因为f(2)=0,所以在(0,2)内恒有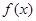 >0;在(2,+∞)内恒有
>0;在(2,+∞)内恒有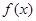 <0.又因为
<0.又因为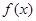 是定义在R上的奇函数,所以在(-∞,-2)内恒有
是定义在R上的奇函数,所以在(-∞,-2)内恒有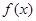 >0;在(-2,0)内恒有
>0;在(-2,0)内恒有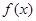 <0.又不等式
<0.又不等式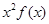 >0的解集,即不等式
>0的解集,即不等式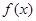 >0的解集.所以答案为(-∞,-2)∪(0,2).故选B.
>0的解集.所以答案为(-∞,-2)∪(0,2).故选B.点评:本题主要考查函数求导法则及函数单调性与导数的关系,同时考查了奇偶函数的图象特征

练习册系列答案
相关题目
 ,满足
,满足 >
> ,则
,则 与
与 的大小关系是( )
的大小关系是( )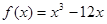 ,若
,若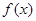 在区间
在区间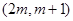 上单调递减,则实数
上单调递减,则实数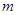 的取值范围是( )
的取值范围是( )



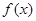 是连续的偶函数,且当
是连续的偶函数,且当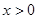 时,
时,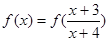 的所有
的所有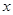 之和为( )
之和为( )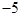
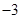
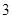
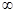 ,+
,+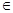 R,则( )
R,则( )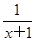 的单调区间为___________.
的单调区间为___________.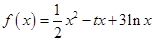 ,
, ,已知
,已知 为函数
为函数 的极值点
的极值点
 在
在 上的单调区间,并说明理由.
上的单调区间,并说明理由. 处的切线斜率为-4,且方程
处的切线斜率为-4,且方程 有两个不相等的负实根,求实数
有两个不相等的负实根,求实数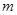 的取值范围.
的取值范围.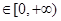 时f(x)是增函数,则f(-2),f(
时f(x)是增函数,则f(-2),f( ),f(-3)的大小关系是:( )
),f(-3)的大小关系是:( )