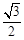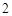题目内容
已知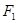 、
、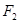 分别为椭圆
分别为椭圆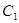 :
: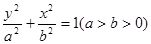 的上、下焦点,其中
的上、下焦点,其中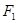 也是抛物线
也是抛物线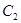 :
: 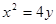 的焦点,点
的焦点,点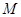 是
是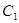 与
与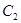 在第二象限的交点,且
在第二象限的交点,且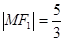 。
。
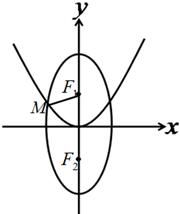
(Ⅰ)求椭圆的方程;
(Ⅱ)已知点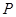 (1,3)和圆
(1,3)和圆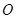 :
: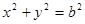 ,过点
,过点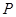 的动直线
的动直线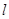 与圆
与圆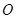 相交于不同的两点
相交于不同的两点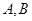 ,在线段
,在线段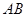 取一点
取一点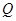 ,满足:
,满足: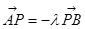 ,
,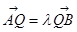 (
(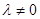 且
且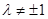 )。
)。
求证:点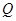 总在某定直线上。
总在某定直线上。
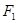 、
、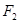 分别为椭圆
分别为椭圆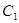 :
: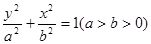 的上、下焦点,其中
的上、下焦点,其中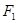 也是抛物线
也是抛物线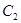 :
: 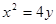 的焦点,点
的焦点,点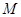 是
是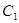 与
与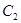 在第二象限的交点,且
在第二象限的交点,且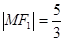 。
。
(Ⅰ)求椭圆的方程;
(Ⅱ)已知点
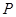 (1,3)和圆
(1,3)和圆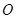 :
: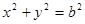 ,过点
,过点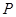 的动直线
的动直线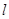 与圆
与圆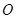 相交于不同的两点
相交于不同的两点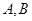 ,在线段
,在线段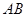 取一点
取一点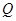 ,满足:
,满足: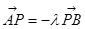 ,
,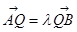 (
(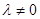 且
且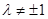 )。
)。求证:点
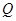 总在某定直线上。
总在某定直线上。(Ⅰ) (Ⅱ)设
(Ⅱ)设 由
由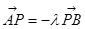 可得
可得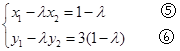 由
由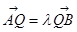 可得
可得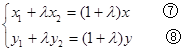 ⑤×⑦得:
⑤×⑦得: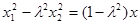 ,⑥×⑧得:
,⑥×⑧得: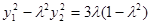 ,两式相加得
,两式相加得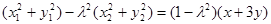 又点A,B在圆
又点A,B在圆 上,且
上,且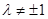 ,
,
所以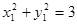 ,
,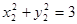 即
即 ,所以点Q总在定直线
,所以点Q总在定直线 上
上
 (Ⅱ)设
(Ⅱ)设 由
由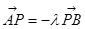 可得
可得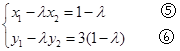 由
由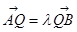 可得
可得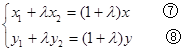 ⑤×⑦得:
⑤×⑦得: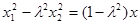 ,⑥×⑧得:
,⑥×⑧得: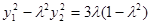 ,两式相加得
,两式相加得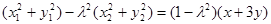 又点A,B在圆
又点A,B在圆 上,且
上,且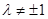 ,
,所以
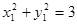 ,
,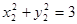 即
即 ,所以点Q总在定直线
,所以点Q总在定直线 上
上试题分析:(1)由
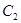 :
: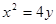 知
知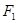 (0,1),设
(0,1),设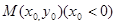 ,因M在抛物线
,因M在抛物线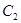 上,故
上,故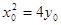 ① 又
① 又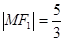 ,则
,则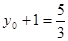 ②,
②,由①②解得
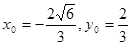 (3分)
(3分)椭圆
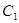 的两个焦点
的两个焦点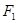 (0,1),
(0,1), ,点M在椭圆上,有椭圆定义可得
,点M在椭圆上,有椭圆定义可得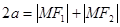
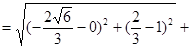

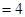
∴
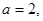 又
又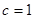 ,∴
,∴ ,椭圆
,椭圆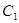 的方程为:
的方程为: (6分)
(6分)(2)设
 ,
,由
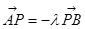 可得:
可得: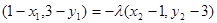 ,
,即
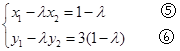 (9分)
(9分)由
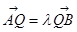 可得:
可得: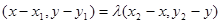 ,
,即
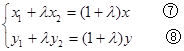
⑤×⑦得:
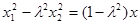
⑥×⑧得:
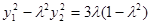 (10分)
(10分)两式相加得
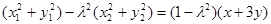 (11分)
(11分)又点A,B在圆
 上,且
上,且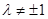 ,
,所以
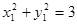 ,
,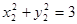
即
 ,所以点Q总在定直线
,所以点Q总在定直线 上 (12分)
上 (12分)点评:解题时充分利用抛物线的定义:抛物线上的点到焦点的距离等于到准线的距离,能使解题过程简化;第二问中的向量关系常转化为点的坐标关系,证明点在定直线上的主要思路是验证点的坐标始终满足于某直线方程

练习册系列答案
相关题目
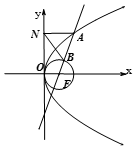
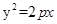 (p>0)的焦点为F,A为C上的点,以F为圆心,
(p>0)的焦点为F,A为C上的点,以F为圆心,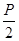 为半径的圆与线段AF的交点为B,∠AFx=60°,A在y轴上的射影为N,则∠
为半径的圆与线段AF的交点为B,∠AFx=60°,A在y轴上的射影为N,则∠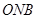 = .
= .
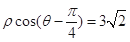 ,曲线
,曲线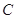 :
: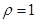 上的点到直线的距离为
上的点到直线的距离为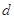 ,则
,则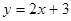 与抛物线
与抛物线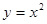 所围成的图形面积是( )
所围成的图形面积是( )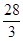
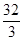
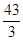
 (
( >0)的顶点作两条互相垂直的弦OA、OB。
>0)的顶点作两条互相垂直的弦OA、OB。
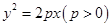 的准线经过椭圆
的准线经过椭圆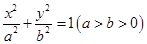 的左焦点,且经过抛物线与椭圆两个交点的弦过抛物线的焦点,则椭圆的离心率为_____________
的左焦点,且经过抛物线与椭圆两个交点的弦过抛物线的焦点,则椭圆的离心率为_____________ ,
, 为双曲线
为双曲线 的右焦点,点
的右焦点,点 ,
, 为
为 轴正半轴上的动点。
轴正半轴上的动点。 的最大值为( )
的最大值为( )



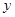 轴上,渐近线方程为
轴上,渐近线方程为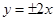 的双曲线的离心率为_______.
的双曲线的离心率为_______.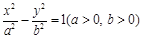 左焦点
左焦点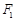 的直线与以右焦点
的直线与以右焦点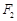 为圆心、
为圆心、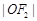 为半径的圆相切于A点,且
为半径的圆相切于A点,且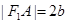 ,则双曲线的离心率为
,则双曲线的离心率为