题目内容
如图,过抛物线 (
(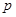 >0)的顶点作两条互相垂直的弦OA、OB。
>0)的顶点作两条互相垂直的弦OA、OB。
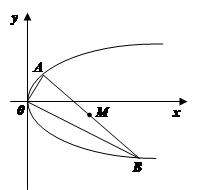
⑴设OA的斜率为k,试用k表示点A、B的坐标;
⑵求弦AB中点M的轨迹方程。
 (
(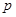 >0)的顶点作两条互相垂直的弦OA、OB。
>0)的顶点作两条互相垂直的弦OA、OB。
⑴设OA的斜率为k,试用k表示点A、B的坐标;
⑵求弦AB中点M的轨迹方程。
⑴A(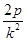 ,
, ),B(
),B(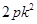 ,
,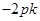 )。⑵
)。⑵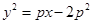 ,即为M点轨迹的普通方程。
,即为M点轨迹的普通方程。
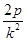 ,
, ),B(
),B(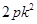 ,
,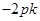 )。⑵
)。⑵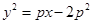 ,即为M点轨迹的普通方程。
,即为M点轨迹的普通方程。试题分析:⑴.∵依题意可知直线OA的斜率存在且不为0
∴设直线OA的方程为
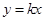 (
(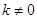 )∴联立方程
)∴联立方程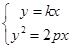
解得
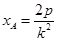
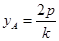 ;以
;以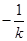 代上式中的
代上式中的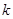 ,解方程组
,解方程组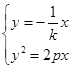
解得
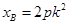
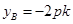 ∴A(
∴A(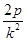 ,
, ),B(
),B(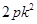 ,
,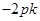 )。 6分
)。 6分⑵.设AB中点M(x,y),则由中点坐标公式,得
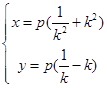
消去参数k,得
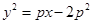 ,即为M点轨迹的普通方程。 12
,即为M点轨迹的普通方程。 12点评:中档题,研究直线与圆锥曲线的位置关系,往往通过建立方程组,应用韦达定理,简化解题过程。“参数法”是求曲线方程的常见方法,通过引入适当的“中间变量”,将动点的坐标相互联系起来。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 和圆
和圆 :
: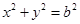 ,过椭圆上一点P引圆O的两条切线,切点分别为A,B.
,过椭圆上一点P引圆O的两条切线,切点分别为A,B. 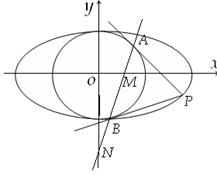
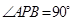 ,求椭圆离心率e的取值范围;
,求椭圆离心率e的取值范围;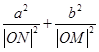 是否为定值?请证明你的结论.
是否为定值?请证明你的结论.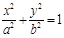 (
( )经过
)经过 与
与 两点.
两点.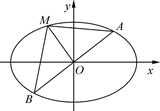
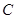 的方程;
的方程;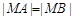 .求证:
.求证: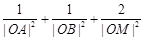 为定值.
为定值.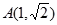 是离心率为
是离心率为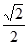 的椭圆
的椭圆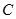 :
: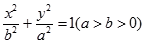 上的一点,斜率为
上的一点,斜率为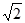 的直线
的直线 交椭圆
交椭圆 、
、 两点,且
两点,且 、
、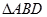 的面积是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由?
的面积是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由?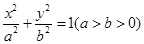 的离心率为
的离心率为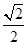 ,且经过点
,且经过点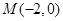 .
.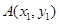 ,
,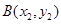 两点,连接MA,MB并延长交直线x=4于P,Q两点,设yP,yQ分别为点P,Q的纵坐标,且
两点,连接MA,MB并延长交直线x=4于P,Q两点,设yP,yQ分别为点P,Q的纵坐标,且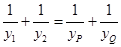 .求△ABM的面积.
.求△ABM的面积. 、
、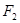 分别为椭圆
分别为椭圆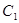 :
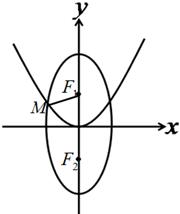
: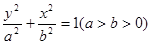 的上、下焦点,其中
的上、下焦点,其中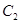 :
: 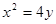 的焦点,点
的焦点,点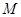 是
是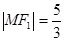 。
。
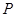 (1,3)和圆
(1,3)和圆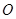 :
: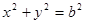 ,过点
,过点 与圆
与圆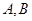 ,在线段
,在线段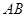 取一点
取一点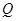 ,满足:
,满足: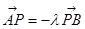 ,
,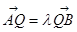 (
(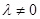 且
且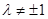 )。
)。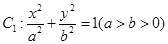 的长轴长为
的长轴长为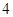 ,离心率为
,离心率为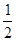 ,
,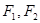 分别为其左右焦点.一动圆过点
分别为其左右焦点.一动圆过点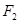 ,且与直线
,且与直线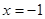 相切.
相切. 及动圆圆心轨迹
及动圆圆心轨迹 的方程;
的方程; 、
、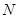 ,椭圆
,椭圆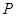 、
、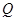 ,满足
,满足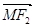 与
与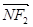 共线,
共线,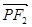 与
与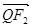 共线,且
共线,且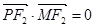 ,求四边形
,求四边形 面积的最小值.
面积的最小值.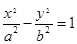 (
( )的两个焦点,若F1、F2、P(0,2
)的两个焦点,若F1、F2、P(0,2 )是正三角形的三个顶点,则双曲线离心率是( )
)是正三角形的三个顶点,则双曲线离心率是( )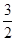
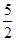
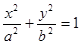
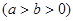 的短轴长等于焦距,椭圆C上的点到右焦点
的短轴长等于焦距,椭圆C上的点到右焦点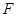 的最短距离为
的最短距离为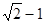 .
.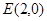 且斜率为
且斜率为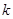 (
(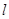 与C交于
与C交于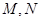 两点,
两点,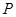 是点
是点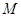 关于
关于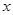 轴的对称点,证明:
轴的对称点,证明: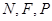 三点共线.
三点共线.