题目内容
已知椭圆 的中心在坐标原点,焦点在
的中心在坐标原点,焦点在 轴上,椭圆
轴上,椭圆 上的点到焦点距离的最大值为
上的点到焦点距离的最大值为 ,最小值为
,最小值为 .
.
(Ⅰ)求椭圆 的标准方程;
的标准方程;
(Ⅱ)若直线 与椭圆
与椭圆 相交于
相交于 ,
, 两点(
两点(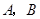 不是左右顶点),且以
不是左右顶点),且以 为直径的圆过椭圆
为直径的圆过椭圆 的右顶点,求证:直线
的右顶点,求证:直线 过定点,并求出该定点的坐标.
过定点,并求出该定点的坐标.
 的中心在坐标原点,焦点在
的中心在坐标原点,焦点在 轴上,椭圆
轴上,椭圆 上的点到焦点距离的最大值为
上的点到焦点距离的最大值为 ,最小值为
,最小值为 .
.(Ⅰ)求椭圆
 的标准方程;
的标准方程;(Ⅱ)若直线
 与椭圆
与椭圆 相交于
相交于 ,
, 两点(
两点(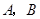 不是左右顶点),且以
不是左右顶点),且以 为直径的圆过椭圆
为直径的圆过椭圆 的右顶点,求证:直线
的右顶点,求证:直线 过定点,并求出该定点的坐标.
过定点,并求出该定点的坐标.(I)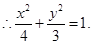
(II)当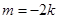 时,
时,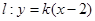 ,直线过定点
,直线过定点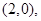 与已知矛盾;当
与已知矛盾;当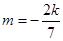 时,
时,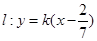 ,直线过定点
,直线过定点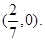
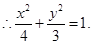
(II)当
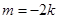 时,
时,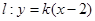 ,直线过定点
,直线过定点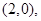 与已知矛盾;当
与已知矛盾;当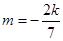 时,
时,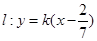 ,直线过定点
,直线过定点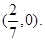
(1)根据椭圆的性质得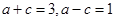 ,所以
,所以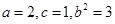 即可写出椭圆的方程.(2)直线
即可写出椭圆的方程.(2)直线 与椭圆
与椭圆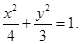 联立消去
联立消去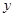 得
得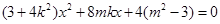 .设
.设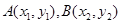 ,由判别式大于0得
,由判别式大于0得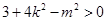 ,利用跟与系数的关系得
,利用跟与系数的关系得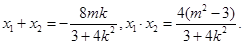 以AB为直径的圆过椭圆的右顶点
以AB为直径的圆过椭圆的右顶点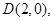 就是
就是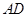 与
与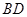 垂直,即
垂直,即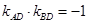 .代入坐标运算可整理得
.代入坐标运算可整理得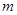 与
与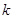 的关系,保证判别式大于0,且直线不过椭圆的左右顶点,得直线过定点
的关系,保证判别式大于0,且直线不过椭圆的左右顶点,得直线过定点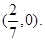
解:(I)由题意设椭圆的标准方程为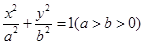
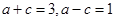 ,
,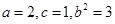
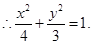
(II)设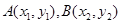 ,由
,由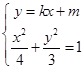 得
得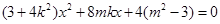 ,
,
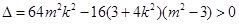 ,
,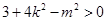 .
.
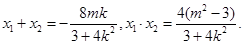
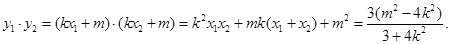
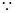 以AB为直径的圆过椭圆的右顶点
以AB为直径的圆过椭圆的右顶点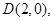
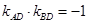 ,
,
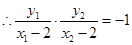 ,
,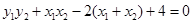 ,
,
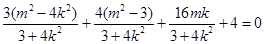 ,
,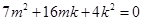 ,解得
,解得
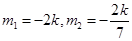 ,且满足
,且满足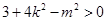 .当
.当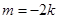 时,
时,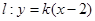 ,直线过定点
,直线过定点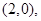 与已知矛盾;当
与已知矛盾;当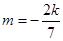 时,
时,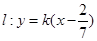 ,直线过定点
,直线过定点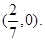
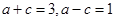 ,所以
,所以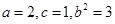 即可写出椭圆的方程.(2)直线
即可写出椭圆的方程.(2)直线 与椭圆
与椭圆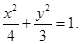 联立消去
联立消去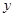 得
得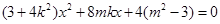 .设
.设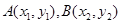 ,由判别式大于0得
,由判别式大于0得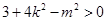 ,利用跟与系数的关系得
,利用跟与系数的关系得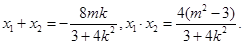 以AB为直径的圆过椭圆的右顶点
以AB为直径的圆过椭圆的右顶点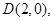 就是
就是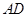 与
与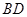 垂直,即
垂直,即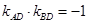 .代入坐标运算可整理得
.代入坐标运算可整理得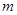 与
与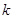 的关系,保证判别式大于0,且直线不过椭圆的左右顶点,得直线过定点
的关系,保证判别式大于0,且直线不过椭圆的左右顶点,得直线过定点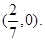
解:(I)由题意设椭圆的标准方程为
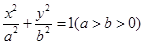
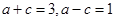 ,
,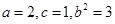
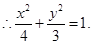
(II)设
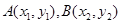 ,由
,由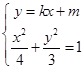 得
得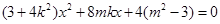 ,
,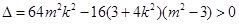 ,
,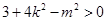 .
.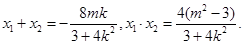
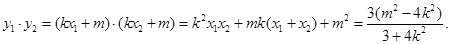
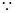 以AB为直径的圆过椭圆的右顶点
以AB为直径的圆过椭圆的右顶点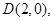
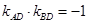 ,
,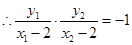 ,
,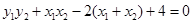 ,
,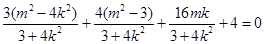 ,
,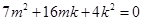 ,解得
,解得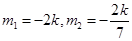 ,且满足
,且满足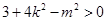 .当
.当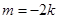 时,
时,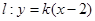 ,直线过定点
,直线过定点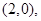 与已知矛盾;当
与已知矛盾;当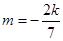 时,
时,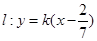 ,直线过定点
,直线过定点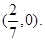

练习册系列答案
相关题目
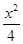 +
+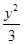 =1的右焦点到直线y=
=1的右焦点到直线y=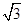 x的距离是 ( )
x的距离是 ( )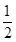
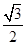
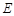 的普通方程为
的普通方程为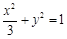
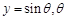 为参数,求椭圆
为参数,求椭圆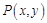 是椭圆
是椭圆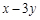 的取值范围.
的取值范围. 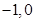 ),(1,0),椭圆的长半轴长为2,则椭圆方程为( )
),(1,0),椭圆的长半轴长为2,则椭圆方程为( )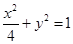
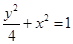
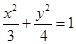
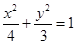
 +
+ =1的离心率 e =
=1的离心率 e = , 则k的值是
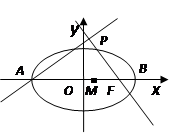
, 则k的值是 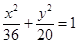 的长轴的左右端点,点F为椭圆的右焦点,直线PF的方程为:
的长轴的左右端点,点F为椭圆的右焦点,直线PF的方程为: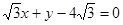 且
且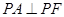 .
.
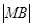 ,求椭圆上的点到点M的距离d的最小值.
,求椭圆上的点到点M的距离d的最小值.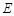 的两焦点分别为
的两焦点分别为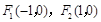 ,且椭圆上的点到
,且椭圆上的点到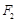 的最小距离为
的最小距离为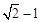 .
.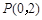 作直线
作直线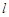 交椭圆
交椭圆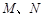 两点,设线段
两点,设线段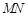 的中垂线交
的中垂线交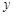 轴于
轴于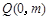 ,求m的取值范围.
,求m的取值范围.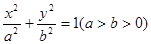 的左焦点
的左焦点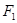 作
作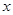 轴的垂线交椭圆于点
轴的垂线交椭圆于点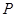 ,
,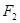 为右焦点,若
为右焦点,若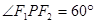 ,则椭圆的离心率为__________________ .
,则椭圆的离心率为__________________ . 的离心率为( )
的离心率为( )


