题目内容
7.已知在($\root{3}{x}$-$\frac{1}{2\root{3}{x}}$)n(n∈N*)的展开式中,第6项为常数项.(1)求n的值及展开式中含x2的项的系数;
(2)①求展开式中所有有理项;
②求展开式中系数的绝对值最大的项.
分析 (1)根据第六项为常数项,x的幂指数为零,求得n的值,在通项公式中,令x的幂指数为2,可得展开式中含x2的项的系数.
(2))①令x的幂指数为整数,求得自然数r的值,可得展开式中有理项.
②设展开式中第r+1项系数的绝对值最大,由(1)知$\left\{\begin{array}{l}{{(\frac{1}{2})}^{r-1}{•C}_{10}^{r-1}{≤(\frac{1}{2})}^{r}{•C}_{10}^{r}}\\{{(\frac{1}{2})}^{r+1}{•C}_{10}^{r+1}{≤(\frac{1}{2})}^{r}{•C}_{10}^{r}}\end{array}\right.$,求得r的范围,可得整数r的值,从而得到展开式中系数的绝对值最大的项.
解答 解:(1)由题意可得T6=${C}_{n}^{5}$•${x}^{\frac{n-5}{3}}$•${(-\frac{1}{2}{•x}^{-\frac{1}{3}})}^{5}$=-$\frac{1}{32}$•${C}_{n}^{5}$•${x}^{\frac{n-10}{3}}$ 为常数项,故有n-10=0,∴n=10.
故通项公式为 Tr+1=${C}_{10}^{r}$•${(-\frac{1}{2})}^{r}$•${x}^{\frac{10-2r}{3}}$,令$\frac{10-2r}{3}$=2,求得r=2,故展开式中含x2的项的系数为$\frac{1}{4}$•${C}_{10}^{2}$=$\frac{45}{4}$.
(2)①由(1)知$\frac{10-2r}{3}$ 为整数,且r=0,1,2,3,…10,故r=2,5,8,
∴展开式中有理项为 T3=$\frac{45}{4}$x2,T6=-$\frac{63}{8}$,T9=$\frac{5}{25{6x}^{2}}$.
②设展开式中第r+1项系数的绝对值最大,由(1)知$\left\{\begin{array}{l}{{(\frac{1}{2})}^{r-1}{•C}_{10}^{r-1}{≤(\frac{1}{2})}^{r}{•C}_{10}^{r}}\\{{(\frac{1}{2})}^{r+1}{•C}_{10}^{r+1}{≤(\frac{1}{2})}^{r}{•C}_{10}^{r}}\end{array}\right.$,
解得 $\frac{8}{3}$≤r≤$\frac{11}{3}$,又r为整数,所以r=3,展开式中系数的绝对值最大的项为T4=-15${x}^{\frac{4}{3}}$.
点评 本题主要考查二项式定理的应用,二项式系数的性质,二项式展开式的通项公式,属于中档题.

| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | 4 | D. | 12 |
| A. | x-2y=0 | B. | 2x-y-3=0 | C. | x-y+1=0 | D. | x-y-1=0 |
| A. | 外切 | B. | 内切 | C. | 相离 | D. | 相交 |
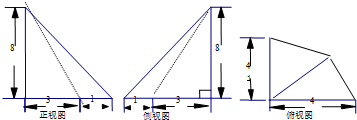 已知某空间几何体的三视图如图所示,则该几何体的体积是32.
已知某空间几何体的三视图如图所示,则该几何体的体积是32.