题目内容
19.已知函数f(x)=3sin$\frac{π}{6}$x+2.(1)五点法画出函数f(x)在一个周期上的图象;
(2)y=sinx的图象经过怎样的变换可以得到f(x)的图象;
(3)当x∈[-3,0]时,求f(x)的最值及相应x的值.
分析 (1)利用五点法即可画出函数f(x)在一个周期上的图象;
(2)根据三角函数的图象关系即可得到结论.
(3)结合三角函数的图象和性质即可得到结论.
解答 解:(1)列表:
| $\frac{π}{6}$x | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| x | 0 | 3 | 6 | 9 | 12 |
| y | 2 | 5 | 2 | -1 | 2 |
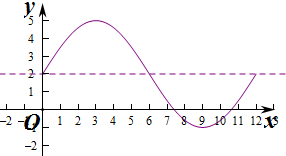
…(6分)
(说明:图象不准确,坐标系元素不全等适当扣1到2分)
(2)将y=sinx的图象上各点的横坐标伸长到原来的$\frac{6}{π}$倍(纵坐标不变)得到y=sin$\frac{π}{6}$x的图象,
再将y=sin$\frac{π}{6}$x的图象上各点的纵坐标伸长到原来的3倍(横坐标不变)得到y=3sin$\frac{π}{6}$x的图象,
然后将y=3sin$\frac{π}{6}$x的图象向上平移2个单位得到函数f(x)的图象.…(10分)
(3)当x∈[-3,0]时,$\frac{π}{6}$x∈[-$\frac{π}{2}$,0],
所以sin$\frac{π}{6}$x∈[-1,0].
即当x=-3时,f(x)取得最小值-1;
当x=0时,f(x)取得最大值2.…(14分)
点评 本题主要考查三角函数的图象和性质,利用五点作图法是解决本题的关键.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
9.在某新型材料的研制中,实验人员获得了如下一组实验数据:现准备下列四个函数中的一个近似地表示这些数据的规律,其中最接近的一个是( )
| X | 1.99 | 3 | 4 | 5.1 | 6.12 |
| Y | 1.5 | 4.04 | 7.5 | 12 | 18.01 |
| A. | y=2x-1 | B. | log2x | C. | y=$\frac{1}{2}({x}^{2}-1)$ | D. | y=($\frac{1}{2}$)x |