题目内容
11．锐角三角形的三边分别为3，5，x，则x的范围是（4，$\sqrt{34}$）．分析 通过余弦定理分别表示出cosC，cosA和cosB，令其大于0求得x的范围．
解答 解：根据题意知$\left\{\begin{array}{l}{cosC=\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}=\frac{9+25-{x}^{2}}{30}＞0}\\{cosA=\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}=\frac{25+{x}^{2}-9}{10x}＞0}\\{cosB=\frac{9+{x}^{2}-25}{6x}＞0}\end{array}\right.$，
解不等式得4＜x＜$\sqrt{34}$，
故答案为：（4，$\sqrt{34}$）
点评 本题主要考查了余弦定理的应用．注重了对余弦定理公式灵活运用的考查．
练习册系列答案
阅读快车系列答案
相关题目
5．设a∈R，若函数y=ex+2ax，x∈R有大于0的极值点，则（ ）
| A． | a＜-$\frac{1}{e}$ | B． | a＞-$\frac{1}{e}$ | C． | a＜-$\frac{1}{2}$ | D． | a＞-$\frac{1}{2}$ |
6．下列说法正确的是（ ）
| A． | 若f′（x0）不存在，则曲线y=f（x）在点（x0，y0）处就没有切线 | |
| B． | 若曲线y=f（x）在点（x0，y0）处有切线，则f′（x0）必存在 | |
| C． | 若f′（x0）不存在，则曲线y=f（x）在点（x0，y0）处的切线斜率不存在 | |
| D． | 若曲线y=f（x）在点（x0，y0）处没有切线，则f′（x0）有可能存在 |
16．某中学有甲乙两个文科班进行数学考试，按照大于或等于120分为优秀，120分以下为非优秀统计成绩后，得到如下列联表：
（Ⅰ）用分层抽样的方法在优秀的学生中抽6人，其中甲班抽多少人？
（Ⅱ）在上述抽取的6人中选2人，求恰有一名同学在乙班的概率；
（Ⅲ）计算出统计量k2，若按95%可靠性要求能否认为“成绩与班级有关”．
下面的临界值表代参考：
（参考公式k2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$其中n=a+b+c+d）
| 优秀 | 非优秀 | 合计 | |
| 甲 | 20 | 5 | 25 |
| 乙 | 10 | 15 | 25 |
| 合计 | 30 | 20 | 50 |
（Ⅱ）在上述抽取的6人中选2人，求恰有一名同学在乙班的概率；
（Ⅲ）计算出统计量k2，若按95%可靠性要求能否认为“成绩与班级有关”．
下面的临界值表代参考：
| P（K2≥k） | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
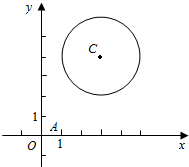已知圆C：ABCD，直线l1过定点A （1，0）．