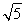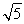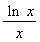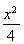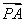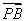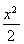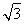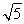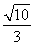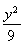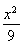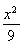题目内容
过抛物线y2=2px(p>0)的焦点F的直线l与抛物线在第一象限的交点为A,直线与抛物线的准线的交点为B,点A在抛物线的准线上的射影为C,若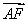 =
=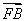 ,
,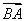 ·
·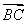 =36,则抛物线的方程为________.
=36,则抛物线的方程为________.
y2=2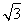 x
x
【解析】设A(x0,y0),则点A关于点F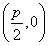 的对称点B的坐标为(p-x0,-y0),该点在抛物线的准线x=-
的对称点B的坐标为(p-x0,-y0),该点在抛物线的准线x=-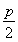 上,所以p-x0=-
上,所以p-x0=-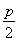 ,即x0=
,即x0=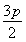 ,此时B
,此时B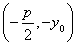 .点C
.点C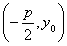 .所以
.所以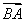 =(2p,2y0),
=(2p,2y0),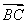 =(0,2y0),因为
=(0,2y0),因为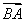 ·
·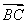 =36,所以4
=36,所以4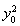 =36,解得y0=3(舍去负值),此时点A
=36,解得y0=3(舍去负值),此时点A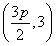 ,代入抛物线方程,得9=3p2,解得p=
,代入抛物线方程,得9=3p2,解得p=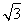 ,所以所求的抛物线方程为y2=2
,所以所求的抛物线方程为y2=2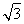 x.
x.

练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目