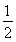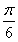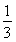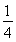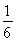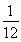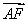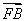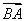题目内容
如图所示,已知椭圆C: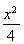 +y2=1,在椭圆C上任取不同两点A,B,点A关于x轴的对称点为A′,当A,B变化时,如果直线AB经过x轴上的定点T(1,0),则直线A′B经过x轴上的定点为________.
+y2=1,在椭圆C上任取不同两点A,B,点A关于x轴的对称点为A′,当A,B变化时,如果直线AB经过x轴上的定点T(1,0),则直线A′B经过x轴上的定点为________.

(4,0)
【解析】设直线AB的方程为x=my+1,由 得(my+1)2+4y2=4,即(m2+4)y2+2my-3=0.
得(my+1)2+4y2=4,即(m2+4)y2+2my-3=0.
记A(x1,y1),B(x2,y2),则A′(x1,-y1),且y1+y2=-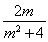 ,y1y2=-
,y1y2=-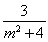 ,
,
当m≠0时,经过点A′(x1,-y1),B(x2,y2)的直线方程为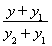 =
=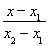 .令y=0,得x=
.令y=0,得x=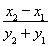 y1+x1=
y1+x1=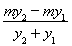 y1+my1+1=
y1+my1+1=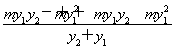 +1=
+1=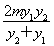 +1=
+1= +1=4,所以y=0时,x=4.
+1=4,所以y=0时,x=4.
当m=0时,直线AB的方程为x=1,此时A′,B重合,经过A′,B的直线有无数条,当然可以有一条经过点(4,0)的直线.当直线AB为x轴时,直线A′B就是直线AB,即x轴,这条直线也经过点(4,0).综上所述,当点A,B变化时,直线A′B经过x轴上的定点(4,0).

练习册系列答案
相关题目