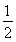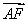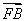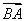题目内容
若函数f(x)＝x3－3x在(a，6－a2)上有最小值，则实数a的取值范围是( )
A．(－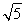
，1) B．[－
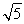，1)
C．[－2，1) D．(－2，1)
C
【解析】由f′(x)＝3x2－3＝0，得x＝±1，且x＝1为函数的极小值点，x＝－1为函数的极大值点．函数f(x)在区间(a，6－a2)上有最小值，则函数f(x)的极小值点必在区间(a，6－a2)内，且左端点的函数值不小于f(1)，即实数a满足a<1<6－a2且f(a)＝a3－3a≥f(1)＝－2，即
解得
故实数a的取值范围是[－2，1)．
练习册系列答案
字词句段篇系列答案
相关题目
